
【题目】![]() 年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从
年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从![]() 年下半年的会员中随机调查了
年下半年的会员中随机调查了![]() 个会员,得到会员对售后服务的满意度评分如下:
个会员,得到会员对售后服务的满意度评分如下:
![]()
根据会员满意度评分,将会员的满意度从低到高分为三个等级:
满意度评分 | 低于 |
| 不低于 |
满意度等级 | 不满意 | 比较满意 | 非常满意 |
(1)根据这![]() 个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
(2)以(1)中的频率作为概率,假设每个会员的评价结果相互独立.
(i)若从下半年的所有会员中随机选取![]() 个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
(ii)若从下半年的所有会员中随机选取![]() 个会员,记评分非常满意的会员的个数为
个会员,记评分非常满意的会员的个数为![]() ,求
,求![]() 的分布列,数学期望
的分布列,数学期望![]() 及方差
及方差![]() .
.
【答案】(1)可估算该购物网店会员对售后服务比较满意和非常满意的频率分别为![]() 和
和![]() ;(2)(i)0.272;(ii)见解析.
;(2)(i)0.272;(ii)见解析.
【解析】试题分析: (1)由给出的![]() 个数据可得,非常满意的个数为
个数据可得,非常满意的个数为![]() ,不满意的个数为
,不满意的个数为![]() ,比较满意的个数为
,比较满意的个数为![]() ,由此可估算该购物网站会员对售后服务比较满意和非常满意的频率;
,由此可估算该购物网站会员对售后服务比较满意和非常满意的频率;
(2)记“恰好一个评分比较满意,另一个评分非常满意”为事件![]() ,则
,则![]() .
.
(ii)![]() 的可能取值为
的可能取值为![]() ,由题意,随机变量
,由题意,随机变量![]()
由此能求出![]() 的分布列,数学期望
的分布列,数学期望![]() 及方差
及方差![]() .
.
试题解析:(1)由给出的![]() 个数据可得,非常满意的个数为
个数据可得,非常满意的个数为![]() ,不满意的个数为
,不满意的个数为![]() ,比较满意的个数为
,比较满意的个数为![]() ,
,
![]() ,
,
![]() 可估算该购物网店会员对售后服务比较满意和非常满意的频率分别为
可估算该购物网店会员对售后服务比较满意和非常满意的频率分别为![]() 和
和![]() ,
,
(2)(i)记“恰好一个评分比较满意,另一个评分非常满意”为事件![]() ,则
,则![]() .
.
(ii)![]() 的可能取值为
的可能取值为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
则![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
由题可知![]() .
.


科目:高中数学 来源: 题型:
【题目】【2018届山西省太原十二中高三上学期1月月考】运动员甲在最近![]() 场
场![]() 比赛中所得分数的茎叶图如图所示,由于疏忽,茎叶图中的两个数据上出行了污渍,导致这两个数字无法辨认,但统计员记得除掉污渍
比赛中所得分数的茎叶图如图所示,由于疏忽,茎叶图中的两个数据上出行了污渍,导致这两个数字无法辨认,但统计员记得除掉污渍![]() 处的数字不影响整体中位数,且这六个数据的平均值为
处的数字不影响整体中位数,且这六个数据的平均值为![]() .
.

(1)求污渍![]() 处的数字;
处的数字;
(2)篮球运动员乙在最近![]() 场
场![]() 的比赛中所得分数为
的比赛中所得分数为![]() .试分别以各自
.试分别以各自![]() 场比赛得分的平均数与方差来分析这两名篮球运动员的发挥水平.
场比赛得分的平均数与方差来分析这两名篮球运动员的发挥水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() ,
, ![]() 分别是椭圆的左、右焦点,以原点为圆心,椭圆
分别是椭圆的左、右焦点,以原点为圆心,椭圆![]() 的短轴长为直径的圆与直线
的短轴长为直径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() ,求
,求![]() 内切圆面积的最大值和此时直线
内切圆面积的最大值和此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=4an﹣p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线的斜率;
处的切线的斜率;
(Ⅱ)判断方程![]() (
(![]() 为
为![]() 的导数)在区间
的导数)在区间![]() 内的根的个数,说明理由;
内的根的个数,说明理由;
(Ⅲ)若函数![]() 在区间
在区间![]() 内有且只有一个极值点,求
内有且只有一个极值点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.
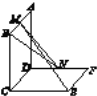
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com