已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn,且有Sn=2bn-1
(1)求{an}、{bn}的通项公式;
(2)若cn=anbn,{cn}的前n项和为Tn,求Tn;
(3)试比较Tn与anSn的大小,并说明理由.
分析:(1)直接利用a3=5,a7=13,列出关于首项和公差的等式,求出首项和公差即可求{an}的通项公式;再利用Sn=2bn-1及Sn-1=2bn-1-1可得bn=2bn-2bn-1,整理得是公比为2 的等比数列,再求出首项即可求{bn}的通项公式;
(2)先整理出{cn}的通项公式,因为是一等差数列乘一等比数列组成的新数列,所以直接利用错位相减法求和即可;
(3)对Tn与anSn作差整理得2(n+1-2n),再研究对应函数f(x)=x+1-2x(x≥1)的单调性求出其最值即可比较出Tn与anSn的大小.
解答:解:(1)∵{a
n}是等差数列,且a
3=5,a
7=13,设公差为d.
∴
,解得
∴a
n=1+2(n-1)=2n-1(n∈N
*)(2分)
在{b
n}中,∵S
n=2b
n-1
当n=1时,b
1=2b
1-1,∴b
1=1
当n≥2时,由S
n=2b
n-1及S
n-1=2b
n-1-1可得b
n=2b
n-2b
n-1,∴b
n=2b
n-1∴{b
n}是首项为1公比为2的等比数列
∴b
n=2
n-1(n∈N
*)(4分)
(2)c
n=a
nb
n=(2n-1)•2
n-1T
n=1+3•2+5•2
2++(2n-1)•2
n-1①
2T
n=1•2+3•2
2+5•2
3++(2n-3)•2
n-1+(2n-1)•2
n②
①-②得-T
n=1+2•2+2•2
2++2•2
n-1-(2n-1)•2
n=
1+2•-(2n-1)•2n=1+4(2
n-1-1)-(2n-1)•2
n=-3-(2n-3)•2
n∴T
n=(2n-3)•2
n+3(n∈N
*)(8分)
(3)T
n-a
nS
n=(2n-3)•2
n+3-(2n-1)(2
n-1)
=(2n-3)•2
n+3-(2n-1)•2
n+2n-1
=2n+2-2•2
n=2(n+1-2
n)(9分)
令f(x)=x+1-2
x(x≥1),则f'(x)=1-2
xln2
∵f'(x)在[1,+∞)是减函数,又f'(1)=1-2ln2=1-ln4<0
∴x≥1时,f'(x)<0
∴x≥1时,f(x)是减函数.
又f(1)=1+1-2=0
∴x≥1时,f(x)≤0
∴x≥1时,x+1-2
x≤0(13分)
∴n∈N
*时,n+1-2
n≤0
∴n∈N
*时,T
n≤a
nS
n(14分)
点评:本题的第二问考查了数列求和的错位相减法.错位相减法适用于通项为一等差数列乘一等比数列组成的新数列.



 阅读快车系列答案
阅读快车系列答案
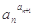 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4