
【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
(Ⅰ) 从III型号汽车的回访客户中随机选取1人,则这个客户不满意的概率为________;
(Ⅱ) 从所有的客户中随机选取1个人,估计这个客户满意的概率;
(Ⅲ) 汽车公司拟改变投资策略,这将导致不同型号汽车的满意率发生变化.假设表格中只有两种型号汽车的满意率数据发生变化,那么哪种型号汽车的满意率增加0.1,哪种型号汽车的满意率减少0.1,使得获得满意的客户人数与样本中的客户总人数的比值达到最大?(只需写出结论)
【答案】(Ⅰ)0.4(Ⅱ)![]() (Ⅲ)增加IV型号汽车的满意率,减少II型号汽车的满意率.
(Ⅲ)增加IV型号汽车的满意率,减少II型号汽车的满意率.
【解析】
(Ⅰ)从III型号汽车的回访客户中随机选取1人,利用对立事件概率计算公式能求出这个客户不满意的概率.(Ⅱ)先求出样本中的回访客户的总数和样本中满意的客户人数,由此能估计这个客户满意的概率.(Ⅲ)增加IV型号汽车的满意率,减少II型号汽车的满意率.
解:(Ⅰ)由表格可知满意的为0.6,所以不满意的为![]()
(Ⅱ)由题意知,样本中的回访客户的总数是![]() ,
,
样本中满意的客户人数是
![]() ,
,
所以样本中客户的满意率为![]() .
.
所以从所有的客户中随机选取1个人,估计这个客户满意的概率为![]() .
.
(Ⅲ)增加IV型号汽车的满意率,减少II型号汽车的满意率.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 在其定义域上为增函数;
在其定义域上为增函数;
②对于任意的![]() ,都有
,都有![]() 成立;
成立;
③![]() 有且仅有两个零点;
有且仅有两个零点;
④若![]() 在点
在点![]() 处的切线也是
处的切线也是![]() 的切线,则
的切线,则![]() 必是
必是![]() 零点.
零点.
其中所有正确的结论序号是( )
A.①②③B.①②C.②③④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与直线
与直线![]() 相切且与圆
相切且与圆![]() 外切。
外切。
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设第一象限内的点![]() 在轨迹
在轨迹![]() 上,若
上,若![]() 轴上两点
轴上两点![]() ,
,![]() ,满足
,满足![]() 且
且![]() . 延长
. 延长![]() 、
、![]() 分别交轨迹
分别交轨迹![]() 于
于![]() 、
、![]() 两点,若直线
两点,若直线![]() 的斜率
的斜率![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为探索课堂教学改革,惠来县某中学数学老师用传统教学和“导学案”两种教学方式,在甲、乙两个平行班进行教学实验.为了解教学效果,期末考试后,分别从两个班级各随机抽取20名学生的成绩进行统计,得到如下茎叶图.记成绩不低于70分者为“成绩优良”.
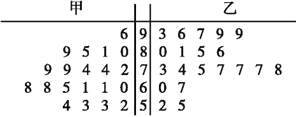
(Ⅰ)分析甲、乙两班的样本成绩,大致判断哪种教学方式的教学效果更佳,并说明理由;
(Ⅱ)由以上统计数据完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
参考公式:![]() ,其中
,其中![]() 是样本容量.
是样本容量.
独立性检验临界值表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点A(-1,0),F(2,0),定直线l:x=![]() ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
(Ⅰ)求E的方程;
(Ⅱ)试判断以线段MN为直径的圆是否过点F,并说明理由.![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
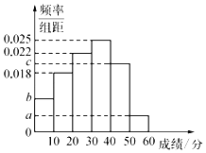
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: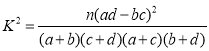 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究患肺癌与是否吸烟有关,某机构做了一次相关调查,制成如下图的![]() 列联表,其中数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的
列联表,其中数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
患肺癌 | 不患肺癌 | 合计 | |
吸烟 | |||
不吸烟 | |||
总计 |
(1)若吸烟不患肺癌的有4人,现从患肺癌的人中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行调查,求这两人都是吸烟患肺癌的概率;
(2)若研究得到在犯错误概率不超过0.001的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)证明:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() .
.
(2)是否存在最大的整数![]() ,使得函数
,使得函数![]() 在其定义域上是增函数?若存在,求
在其定义域上是增函数?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com