
【题目】在平面直角坐标系xOy中,已知圆O:x2+y2=1,O1:(x﹣4)2+y2=4,动点P在直线x+ ![]() y+b=0上,过P分别作圆O,O1的切线,切点分别为A,B,若满足PB=2PA的点P有且只有两个,则实数b的取值范围是 .
y+b=0上,过P分别作圆O,O1的切线,切点分别为A,B,若满足PB=2PA的点P有且只有两个,则实数b的取值范围是 .
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,A为以原点O为圆心的单位圆O与x正半轴的交点,在圆心角为 ![]() 的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ.
的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ. 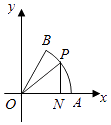
(1)设△PON的面积为y,使y取得最大值时的点P记为E,点N记为F,求此时 ![]() 的值;
的值;
(2)求k=a| ![]() ||
|| ![]() |+
|+ ![]() (a∈R,E 是在(1)条件下的点 E)的值域.
(a∈R,E 是在(1)条件下的点 E)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①y=ax , ②y=bx , ③y=cx , ④y=dx , 根据图象可得a、b、c、d与1的大小关系为( )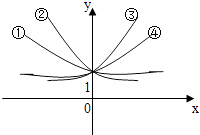
A.a<b<1<c<d
B.b<a<1<d<c
C.1<a<b<c<d
D.a<b<1<d<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx( ![]() sinx+cosx)+m,(x∈R,m∈R).
sinx+cosx)+m,(x∈R,m∈R).
(1)求f(x)的最小正周期;
(2)若f(x)在区间[0, ![]() ]上的最大值是6,求f(x)在区间[0,
]上的最大值是6,求f(x)在区间[0, ![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,PA是四棱锥的高,PB与DC所成角为45°,F是PB的中点,E是BC上的动点.
(Ⅰ)证明:PE⊥AF;
(Ⅱ)若BC=2BE=2 ![]() AB,求直线AP与平面PDE所成角的大小..
AB,求直线AP与平面PDE所成角的大小..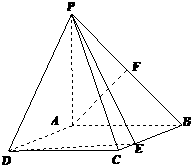
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某等腰三角形的底角为α,顶角为β,且cosβ= ![]() . (Ⅰ)求sinα的值;
. (Ⅰ)求sinα的值;
(Ⅱ)若函数f(x)=tanx在[﹣ ![]() ,α]上的值域与函数g(x)=2sin(2x﹣
,α]上的值域与函数g(x)=2sin(2x﹣ ![]() )在[0,m]上的值域相同,求m的取值范围.
)在[0,m]上的值域相同,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷是德国著名数学家,函数D(x)= ![]() 被称为狄利克雷函数,下面给出关于狄利克雷函数D(x)的五个结论: ①若x是无理数,则D(D(x))=0;
被称为狄利克雷函数,下面给出关于狄利克雷函数D(x)的五个结论: ①若x是无理数,则D(D(x))=0;
②函数D(x)的值域是[0,1];
③函数D(x)偶函数;
④若T≠0且T为有理数,则D(x+T)=D(x)对任意的x∈R恒成立;
⑤存在不同的三个点A(x1 , D(x1)),B(x2 , D(x2)),C(x3 , D(x3)),使得△ABC为等边角形.
其中正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com