
 、
、 、
、 是互不共线的非零向量,则
是互不共线的非零向量,则 -
- =
= ;
; 的解集为[2,+∞);
的解集为[2,+∞);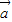 •
• )
) -(
-( •
• )
) =
= 正确,则
正确,则 ,若
,若 与
与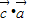 不全为0,则向量
不全为0,则向量 与
与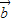 共线,与已知
共线,与已知 、
、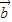 、
、 是互不共线的非零向量矛盾,因此不正确;
是互不共线的非零向量矛盾,因此不正确; ”推不出“tanα=tanβ”;反之也不成立,如
”推不出“tanα=tanβ”;反之也不成立,如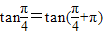 ,但是
,但是 .因此则“α=β”是“tanα=tanβ”的既不充分也不必要条件;
.因此则“α=β”是“tanα=tanβ”的既不充分也不必要条件; ;当x>1时,原不等式可化为x-2≥0,解得x≥2.综上可知:原不等式的解集为{1}∪[2,+∞),故⑤不正确;
;当x>1时,原不等式可化为x-2≥0,解得x≥2.综上可知:原不等式的解集为{1}∪[2,+∞),故⑤不正确;

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二上学期期中考试理科数学 题型:填空题
设α、β、γ是互不重合的平面,m,n是互不重合的直线,给出四个命题:
①若m⊥α,m⊥β,则α∥β
②若α⊥γ,β⊥γ,则α∥β
③若m⊥α,m∥β,则α⊥β ④若m∥α,n⊥α,则m⊥n
其中真命题的序号是______.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:安徽省期中题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com