
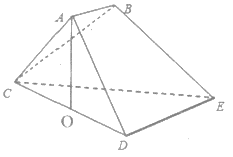
【题目】已知多面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)取CE中点F,连接BF,OF,由几何关系可证得四边形ABFO为平行四边形,结合线面平行的性质定理可得题中的结论;
(Ⅱ)取DE中点M,连接AF,由题意可证得ABEM为平行四边形,从而∠CAM或其补角为AC与BE所成的角.求得三角形的边长,利用余弦定理可得异面直线AC和BE所成角的余弦值.
(Ⅲ)由题意结合(Ⅱ)中的结论可知∠DBF就是直线BD与平面BEC所成角,利用边长的比值关系可得![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅰ)取CE中点F,连接BF,OF,
∵O为CD的中点,
∴OF∥DE,且OF=DE,
∵AB//DE,AC=AD=CD=DE=2,AB=1,
∴OF∥AB,OF=AB,
则四边形ABFO为平行四边形,
∴AO//BF,BF平面BCE,AO平面BCE,
∴AO//平面BCE;
(Ⅱ)取DE中点M,连接AF,
∵AB∥DE,AB=1,DE=2,
∴AB∥ME,AB=ME ,
∴ABEM为平行四边形.
∴AM//BE.
∴∠CAM或其补角为AC与BE所成的角.
∵DE⊥平面ACD,AD,CD平面ACD,
∴DE⊥CD,DE⊥AD,
在![]() 中,CD=2,DM=1,
中,CD=2,DM=1,![]() ,
,
在![]() 中,AD=2,DM=1,
中,AD=2,DM=1,![]() ,
,
![]() .
.
所以异面直线AC和BE所成角的余弦值为![]() .
.
(Ⅲ)由题意可得BF//AO,
∵AO⊥平面CDE,∴BF⊥平面CDE,∴BF⊥DF.
∵CD=DE,∴DF⊥CE,
∵BF∩CE=F,∴DF⊥平面CBE;
∴∠DBF就是直线BD与平面BEC所成角.
在△BDF中,![]() ,
,
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆与抛物线![]() 有一个相同的焦点,且该椭圆的离心率为
有一个相同的焦点,且该椭圆的离心率为![]() ,
,
(Ⅰ)求该椭圆的标准方程:
(Ⅱ)求过点![]() 的直线与该椭圆交于A,B两点,O为坐标原点,若
的直线与该椭圆交于A,B两点,O为坐标原点,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() .
.
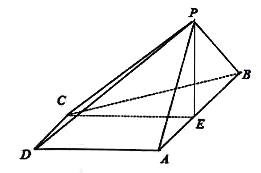
(1)求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通项公式;
(2)若T3=21,求S3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,
的各项均为正数,![]() ,且对任意
,且对任意![]() ,都有
,都有![]() ,数列
,数列![]() 前n项的和
前n项的和![]() .
.
(1)若数列![]() 是等比数列,求
是等比数列,求![]() 的值和
的值和![]() ;
;
(2)若数列![]() 是等差数列,求
是等差数列,求![]() 和
和![]() 的关系式;
的关系式;
(3)![]() ,当
,当![]() 时,求证:
时,求证: ![]() 是一个常数.
是一个常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司新发明了甲、乙两种不同型号的手机,公司统计了消费者对这两种型号手机的评分情况,作出如下的雷达图,则下列说法不正确的是( )
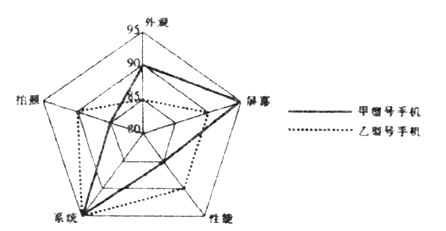
A. 甲型号手机在外观方面比较好.B. 甲、乙两型号的系统评分相同.
C. 甲型号手机在性能方面比较好.D. 乙型号手机在拍照方面比较好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com