练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

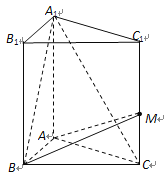
    【题目】直三棱柱中，底面为等腰直角三角形，，，，是侧棱上一点，设．

    (1) 若，求的值；

    (2) 若，求直线与平面所成的角．

    【答案】（1）（2）

    【解析】

    试题（1）以为坐标原点，以射线、、分别为、、轴建立空间直角坐标系，求出，，利用，求出的值；（2）求出直线的方向向量与平面的法向量，求出向量的夹角的余弦值可得结果.

    试题解析：（1）以为坐标原点，以射线、、分别为、、轴建立空间直角坐标系，如图所示，

    则,，，

    ，

    由得，即

    解得．

    (2) 解法一：此时

    设平面的一个法向量为

    由得

    所以

    设直线与平面所成的角为

    则

    所以直线与平面所成的角为

    解法二：联结，则，

    ，平面

    平面

    所以是直线与平面所成的角；

    在中，

    所以

    所以

    所以直线与平面所成的角为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数

    讨论函数的单调性；

    设，对任意的恒成立，求整数的最大值；

    求证：当时，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年以来，世界经济和贸易增长放缓，中美经贸摩擦影响持续显现，我国对外贸易仍然表现出很强的韧性.今年以来，商务部会同各省市全面贯彻落实稳外贸决策部署，出台了一系列政策举措，全力营造法治化国际化便利化的营商环境，不断提高贸易便利化水平，外贸稳规模提质量转动力取得阶段性成效，进出口保持稳中提质的发展势头，如图是某省近五年进出口情况统计图，下列描述错误的是（ ）

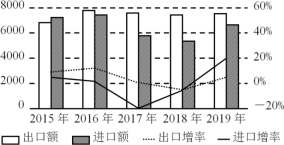
    A.这五年，2015年出口额最少B.这五年，出口总额比进口总额多

    C.这五年，出口增速前四年逐年下降D.这五年，2019年进口增速最快

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线上的点到点的距离比到直线的距离小，为坐标原点.

    （1）过点且倾斜角为的直线与曲线交于、两点，求的面积；

    （2）设为曲线上任意一点，点，是否存在垂直于轴的直线，使得被以为直径的圆截得的弦长恒为定值？若存在，求出的方程和定值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知平面平面，直线平面，且.

    （1）求证：平面；

    （2）若，平面，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，．

    （1）当时，求函数的单调区间；

    （2）若曲线在点(1，0)处的切线为l : x＋y－1＝0，求a，b的值；

    （3）若恒成立，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

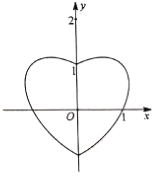
    【题目】数学中有许多形状优美、寓意美好的曲线，如下图就是在平面直角坐标系的“心形曲线”，又名RC心形线.如果以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，其RC心形线的极坐标方程为.

    （1）求RC心形线的直角坐标方程；

    （2）已知与直线（为参数），若直线与RC心形线交于两点，，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了预防新型冠状病毒的传染，人员之间需要保持一米以上的安全距离．某公司会议室共有四行四列座椅，并且相邻两个座椅之间的距离超过一米，为了保证更加安全，公司规定在此会议室开会时，每一行、每一列均不能有连续三人就座．例如下图中第一列所示情况不满足条件（其中“√”表示就座人员）．根据该公司要求，该会议室最多可容纳的就座人数为（ ）

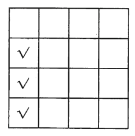
    A.9B.10C.11D.12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）求函数的单调区间；

    （Ⅱ）当时，若在上有零点，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案