
| 1 | 3 |
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
在某校组织的一次篮球定点投篮测试中,规定每人最多投 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在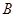 处每投进一球得
处每投进一球得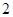 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用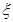 表示,如果
表示,如果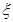 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在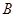 处投;方案2:都在
处投;方案2:都在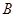 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为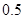 ,在
,在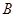 处投篮的命中率为
处投篮的命中率为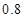 .
.
(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分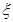 的分布列和数学期望
的分布列和数学期望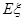 ;
;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:《第3章 概率》2013年单元测试卷(解析版) 题型:填空题
 ,那么他连续投三次,恰好两次投中的概率为 ;至少有一次投中的概率为 (用数字作答).
,那么他连续投三次,恰好两次投中的概率为 ;至少有一次投中的概率为 (用数字作答).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com