
【题目】已知函数![]() .
.
(1)若![]() 是单调递增函数,求实数a的取值范围;
是单调递增函数,求实数a的取值范围;
(2)若![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)求出函数的导数,问题转化为![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() 的范围即可;
的范围即可;
(2)令![]() (
(![]() ),问题等价于
),问题等价于![]() .求导数,判断
.求导数,判断![]() 的单调性,求最值即可.
的单调性,求最值即可.
(1)定义域![]() ,
,![]() ,
,
因为![]() 是单调递增函数,故
是单调递增函数,故![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立.
恒成立.
记![]() ,则
,则![]() ,
,
由![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
所以![]() ,
,
从而![]() .
.
(2)令![]() (
(![]() ),问题等价于
),问题等价于![]() .
.
由![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 上是增函数,
上是增函数,
容易证明![]() 时,
时,![]() ,
,![]() ,
,
则![]() ,
,
由![]() 得,
得, (舍负)
(舍负)
从而取 ,
,![]() ;
;
另外,容易证明![]() ,取正数x满足
,取正数x满足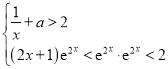
从而取c满足 ,有
,有![]() .
.
(注:这里也可以这样处理:当![]() 时,
时,![]() ,
,![]() ,
,
故![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() )
)
所以存在唯一的![]() ,使得
,使得![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
从而![]() 在区间
在区间![]() 上递减,在
上递减,在![]() 上递增,
上递增,
![]() ,
,
由![]() ,得:
,得:![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
设![]() ,则
,则![]() 为增函数,
为增函数,
![]() ,
,![]() ,则
,则![]() 有唯一零点,设为t,
有唯一零点,设为t,
则![]() ,则
,则![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() 单调递增,且
单调递增,且![]() ,
,
则![]() ,即
,即![]() ,
,
∵![]() 在
在![]() 为增函数,
为增函数,
则当![]() 时,a有最大值,
时,a有最大值,![]() ,
,
∴![]() ,即a的取值范围是
,即a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图![]() ,某十字路口的花圃中央有一个底面半径为
,某十字路口的花圃中央有一个底面半径为![]() 的圆柱形花柱,四周斑马线的内侧连线构成边长为
的圆柱形花柱,四周斑马线的内侧连线构成边长为![]() 的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器
的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器![]() 的移动速度为
的移动速度为![]() ,仪器
,仪器![]() 的移动速度为
的移动速度为![]() .若仪器
.若仪器![]() 与仪器
与仪器![]() 的对视光线被花柱阻挡,则称仪器
的对视光线被花柱阻挡,则称仪器![]() 在仪器
在仪器![]() 的“盲区”中.
的“盲区”中.



(1)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 在点
在点![]() 处,仪器
处,仪器![]() 在
在![]() 上距离点
上距离点![]()
![]() 处,试判断仪器
处,试判断仪器![]() 是否在仪器
是否在仪器![]() 的“盲区”中,并说明理由;
的“盲区”中,并说明理由;
(2)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,同时仪器
移动,同时仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,在这个移动过程中,仪器
移动,在这个移动过程中,仪器![]() 在仪器
在仪器![]() 的“盲区”中的时长为多少?
的“盲区”中的时长为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 、
、![]() 的边长都是1,而且平面
的边长都是1,而且平面![]() 、
、![]() 互相垂直.点M在
互相垂直.点M在![]() 上移动,点N在
上移动,点N在![]() 上移动,若
上移动,若![]() (
(![]() ).
).

(1)当a为何值时,![]() 的长最小;
的长最小;
(2)当![]() 长最小时,求面
长最小时,求面![]() 与面
与面![]() 所成的二面角α的余弦值.
所成的二面角α的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双纽线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线.在平面直角坐标系![]() 中,把到定点
中,把到定点![]() ,
,![]() 距离之积等于
距离之积等于![]() 的点的轨迹称为双纽线
的点的轨迹称为双纽线![]() .已知点
.已知点![]() 是双纽线
是双纽线![]() 上一点,下列说法中正确的有( )
上一点,下列说法中正确的有( )
①双纽线经过原点![]() ; ②双纽线
; ②双纽线![]() 关于原点
关于原点![]() 中心对称;
中心对称;
③![]() ; ④双纽线
; ④双纽线![]() 上满足
上满足![]() 的点
的点![]() 有两个.
有两个.
A.①②B.①②③C.②③D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com