
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() :
:![]()
![]() 的左、右焦点,且椭圆
的左、右焦点,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() .点M、N是椭圆
.点M、N是椭圆![]() 上位于
上位于![]() 轴上方的两点,且向量
轴上方的两点,且向量![]() 与向量
与向量![]() 平行.
平行.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求△
时,求△![]() 的面积;
的面积;
(3)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据椭圆的简单性质可得![]() ,解得即可,
,解得即可,
(2)可设![]() ,
,![]() ,根据向量的数量积求出点
,根据向量的数量积求出点![]() 的坐标,再根据直线平行,求出
的坐标,再根据直线平行,求出![]() 的坐标,
的坐标,
利用两点间的距离公式和点到直线的距离公式和三角形的面积公式计算即可,
(3)向量![]() 与向量
与向量![]() 平行,不妨设
平行,不妨设![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,根据坐标之间的关系,求得
,根据坐标之间的关系,求得![]() 的坐标,再根据向量的模,即可求出
的坐标,再根据向量的模,即可求出![]() 的值,根据斜率公式求出直线的斜率,根据直线平行和点斜式即可求出直线方程.
的值,根据斜率公式求出直线的斜率,根据直线平行和点斜式即可求出直线方程.
解:(1)点![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,
![]() ,
,![]() ,
,
![]() 椭圆
椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 椭圆的方程为
椭圆的方程为![]() ,
,
(2)由(1)可得![]() ,
,![]() ,
,
点![]() 、
、![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的两点,
轴上方的两点,
可设![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
解得![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() 向量
向量![]() 与向量
与向量![]() 平行,
平行,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,
![]() 直线方程为
直线方程为![]() ,
,
联立方程组 ,解得
,解得![]() ,
,![]() (舍去),或
(舍去),或![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
点![]() 到直线直线
到直线直线![]() 的距离为
的距离为![]() ,
,
![]()
![]() 的面积
的面积![]() ,
,
(3)![]() 向量
向量![]() 与向量
与向量![]() 平行,
平行,
![]() ,
,
![]()
![]() ,
,
![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
解得![]() ,或
,或![]() (舍去)
(舍去)
![]() ,
,
![]() ,
,
![]() ,
,
![]()
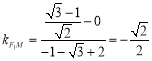 ,
,
![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
即为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下列四个结论:
有下列四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最小正周期为
的最小正周期为![]() ;③
;③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的值域为
的值域为![]() .
.
上述结论中,正确的为( )
A.③④B.②④C.①③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】陕西关中的秦腔表演朴实,粗犷,细腻,深刻,再有电子布景的独有特效,深得观众喜爱.戏曲相关部门特意进行了“喜爱看秦腔”调查,发现年龄段与爱看秦腔的人数比存在较好的线性相关关系,年龄在![]() ,
,![]() ,
,![]() ,
,![]() 的爱看人数比分别是0.10,0.18,0.20,0.30.现用各年龄段的中间值代表年龄段,如42代表
的爱看人数比分别是0.10,0.18,0.20,0.30.现用各年龄段的中间值代表年龄段,如42代表![]() .由此求得爱看人数比
.由此求得爱看人数比![]() 关于年龄段
关于年龄段![]() 的线性回归方程为
的线性回归方程为![]() .那么,年龄在
.那么,年龄在![]() 的爱看人数比为( )
的爱看人数比为( )
A.0.42B.0.39C.0.37D.0.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省新课改后某校为预测2020届高三毕业班的本科上线情况,从该校上一届高三(1)班到高三(5)班随机抽取50人,得到各班抽取的人数和其中本科上线人数,并将抽取数据制成下面的条形统计图.

(1)根据条形统计图,估计本届高三学生本科上线率.
(2)已知该省甲市2020届高考考生人数为4万,假设以(1)中的本科上线率作为甲市每个考生本科上线的概率.
(i)若从甲市随机抽取10名高三学生,求恰有8名学生达到本科线的概率(结果精确到0.01);
(ii)已知该省乙市2020届高考考生人数为3.6万,假设该市每个考生本科上线率均为![]() ,若2020届高考本科上线人数乙市的均值不低于甲市,求p的取值范围.
,若2020届高考本科上线人数乙市的均值不低于甲市,求p的取值范围.
可能用到的参考数据:取![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() 为常数;
为常数;
(1)若![]() ,且
,且![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 个点
个点![]()
![]() ,满足
,满足![]() ,
, ![]() ,
,
![]() ,使得
,使得![]() ,
,
求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 的对称中心为坐标原点,则关于函数
的对称中心为坐标原点,则关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的最小正周期为
的最小正周期为![]() ②若
②若![]() 的最大值为2,则
的最大值为2,则![]()
③![]() 在
在![]() 有两个零点 ④
有两个零点 ④![]() 在区间
在区间![]() 上单调
上单调
其中所有正确结论的标号是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
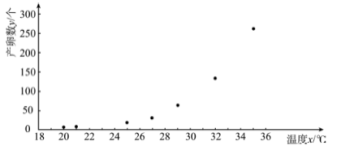
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com