
【题目】某企业在第![]() 年年初购买一台价值为
年年初购买一台价值为![]() 万元的设备
万元的设备![]() ,
,![]() 的价值在使用过程中逐年减少从第
的价值在使用过程中逐年减少从第![]() 年到第
年到第![]() 年,每年年初
年,每年年初![]() 的价值比上年年初减少
的价值比上年年初减少![]() 万元;从第
万元;从第![]() 年开始,每年年初
年开始,每年年初![]() 的价值为上年年初的
的价值为上年年初的![]() .
.
(1)求第![]() 年年初
年年初![]() 的价值
的价值![]() 的表达式.
的表达式.
(2)设![]() ,若
,若![]() 大于
大于![]() 万,则
万,则![]() 继续使用;否则,必须在第
继续使用;否则,必须在第![]() 年年初对
年年初对![]() 更新.
更新.
①求![]() ;
;
②证明:必须在第![]() 年年初对
年年初对![]() 更新.(若
更新.(若![]() 是递减数列,
是递减数列,![]() 也是递减数列).
也是递减数列).
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
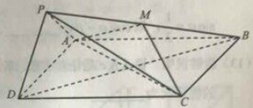
(1)求证:M为PB的中点;
(2)求二面角B-PD-A的大小;
(3)求直线MC与平面BDP所成角的正炫值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加![]() 元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费
元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费![]() 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费![]() 元.
元.
(1)当每辆车的月租金定为![]() 元时,能租出多少辆车?
元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某建筑工程施工期间的降水量![]() (单位:
(单位: ![]() )对工期的影响如下表:
)对工期的影响如下表:

根据某气象站的资料,某调查小组抄录了该工程施工地某月前20天的降水量的数据,绘制得到降水量的折线图,如下图所示.

(1)根据降水量的折线图,分别求该工程施工延误天数![]() 的频率;
的频率;
(2)以(1)中的频率作为概率,求工期延误天数![]() 的分布列及数学期望与方差.
的分布列及数学期望与方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com