
【题目】由0123456可以组成多少个没有重复数字的
(1)五位数;
(2)五位偶数;
(3)能被5整除的五位数.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]()
【解析】
(1)首先在除0外的剩余数中选择一个安排在万位,然后剩余6个数进行全排列;(2)分末位为0与末位不为0两种情况计算可以组成的无重复数字的五位偶数,求和即可;(3)分末位为0与末位为5两种情况求出能组成的被5整除的五位数的个数,求和即可.
(1)首先在除0外的剩余数中选择一个安排在首位,
然后从剩余6个数中选择4个数进行全排列,
共有![]() 种排列方式;
种排列方式;
(2)由0123456可以组成![]() 个末位为0的五位偶数,
个末位为0的五位偶数,
![]() 个末位不为0的五位偶数,
个末位不为0的五位偶数,
所以共可以组成2140个没有重复数字的五位偶数;
(3)末位为0,则前4位从剩余6个数中抽取4个进行全排列,
共能排出![]() 种能被5整除的五位数;
种能被5整除的五位数;
末位为5,首先从1、2、3、4、6中选1个数排在首位,
然后从剩余的5个数中抽取3个数排列在中间三位,
可以组成![]() 个能被5整除的五位数,
个能被5整除的五位数,
所以共可以组成![]() 个能被5整除的五位数.
个能被5整除的五位数.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
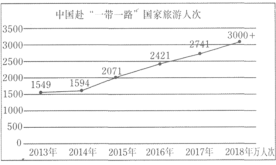
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2016年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为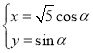 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点F为圆C:
的焦点F为圆C:![]() 的圆心.
的圆心.
![]() 求抛物线的方程与其准线方程;
求抛物线的方程与其准线方程;
![]() 直线l与圆C相切,交抛物线于A,B两点;
直线l与圆C相切,交抛物线于A,B两点;
![]() 若线段AB中点的纵坐标为
若线段AB中点的纵坐标为![]() ,求直线l的方程;
,求直线l的方程;
![]() 求
求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,写出函数
时,写出函数![]() 的单调区间;(直接写出答案,不必写出证明过程)
的单调区间;(直接写出答案,不必写出证明过程)
(2)当![]() 时,求函数
时,求函数![]() 的零点;
的零点;
(3)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对本工厂工人的理论成绩与实践能力进行分析,决定从本工厂工人中随机抽取一个样本容量为7的样本进行分析.如果随机抽取的7名工人的理论成绩与实践能力值![]() 单位:分
单位:分![]() 对应如下表:
对应如下表:
工人序号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
理论成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
实践能力值 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
(1)求这7名工人的理论成绩![]() 与实践能力值
与实践能力值![]() 的中位数、极差;
的中位数、极差;
(2)若规定85分以上![]() 包括85分
包括85分![]() 为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
(3)根据下表数据,求实践能力值y关于理论成绩x的线性回归方程.![]() 系数精确到
系数精确到![]()
附:线性回归方程![]() 中,
中,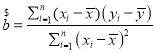 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在微信群中发了一个8元“拼手气”红包,被甲、乙、丙三人抢完,若三人均领到整数元,且每人至少领到1元,则甲领到的钱数不少于其他任何人的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com