
【题目】将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球.其号码为a,放回后,乙从此袋中再摸出一个球,其号码为b,则使不等式a-2b+10>0成立的事件发生的概率等于________.
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,设内角A、B、C的对边分别为a、b、c,向量 ![]() =(cosA+
=(cosA+ ![]() ,sinA),向量
,sinA),向量 ![]() =(﹣sinA,cosA),若|
=(﹣sinA,cosA),若| ![]() +
+ ![]() |=2.
|=2.
(1)求角A的大小;
(2)若b=4 ![]() ,且c=
,且c= ![]() a,求△ABC的面积.
a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知直线![]() 与双曲线
与双曲线![]() 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求![]() 的值及B点坐标;
的值及B点坐标;
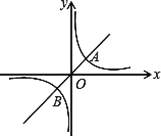
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=cos2x﹣ ![]() sin2x,把y=f(x)的图象向左平移φ(φ>0)个单位后,恰好得到函数g(x)=﹣cos2x﹣
sin2x,把y=f(x)的图象向左平移φ(φ>0)个单位后,恰好得到函数g(x)=﹣cos2x﹣ ![]() sin2x的图象,则φ的值可以为( )
sin2x的图象,则φ的值可以为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2,连结
,如图2,连结![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2+bx+c(a>0),
(1)当a=1,b=2,若|f(x)|﹣2=0有且只有两个不同的实根,求实数c的取值范围;
(2)设方程f(x)=x的两个实根为x1 , x2 , 且满足0<t<x1 , x2﹣x1> ![]() ,试判断f(t)与x1的大小,并给出理由.
,试判断f(t)与x1的大小,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},an≥0,a1=0,an+12+an+1﹣1=an2(n∈N).记Sn=a1+a2+…+an . Tn= ![]() +
+ ![]() +…+
+…+ ![]() .求证:当n∈N*时
.求证:当n∈N*时
(1)0≤an<an+1<1;
(2)Sn>n﹣2;
(3)Tn<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.

(1)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)记F(x)=f(x)﹣g(x),判断F(x)在区间(1,2)内零点个数并说明理由;
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并给出对应的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com