
【题目】直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D. 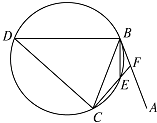
(1)证明:DB=DC;
(2)设圆的半径为1,BC=3,延长CE交AB于点F,求△BCF外接圆的半径.
【答案】
(1)证明:连结DE,交BC于点G.
由弦切角定理得,∠ABE=∠BCE.
而∠ABE=∠CBE,
故∠CBE=∠BCE,BE=CE.
又因为DB⊥BE,
所以DE为直径,∠DCE=90°,
由勾股定理可得DB=DC
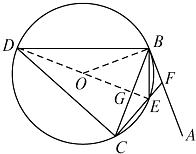
(2)解:由(1)知,∠CDE=∠BDE,DB=DC,
故DG是BC的中垂线,
所以BG= ![]() .
.
设DE的中点为O,连结BO,则∠BOG=60°.
从而∠ABE=∠BCE=∠CBE=30°,
所以CF⊥BF,
故Rt△BCF外接圆的半径等于 ![]() .
.
【解析】(1)构造辅助线DE,交BC于点G.由弦切角定理,圆上的同弧,等弧的性质,通过导角,可以得知∠CBE=∠BCE,BE=CE,又因为DE为直径,即∠DCE=90°,由勾股定理可证得DB=DC;(2)由(1)可得DG是BC的中垂线,即可求得BG的长度.设DE的中点为O,连结BO,求得∠BOG=60°,通过导角,可得CF⊥BF,即可求得Rt△BCF外接圆的半径.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的焦点在圆x2+y2=3上,且离心率为
(a>b>0)的焦点在圆x2+y2=3上,且离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的直线l与椭圆C交于A,B两点,F为右焦点,若△FAB为直角三角形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以双曲线 ![]() (a>0,b>0)上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F,且与y轴交于P、Q两点.若△MPQ为锐角三角形,则该双曲线的离心率e的范围是( )
(a>0,b>0)上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F,且与y轴交于P、Q两点.若△MPQ为锐角三角形,则该双曲线的离心率e的范围是( )
A.![]()
B.( ![]() ,
, ![]() )
)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,方程f(x)=0有3个不同的根.
,方程f(x)=0有3个不同的根.
(1)求实数m的取值范围;
(2)是否存在实数m,使得f(x)在(0,1)上恰有两个极值点x1 , x2且满足x2=2x1 , 若存在,求实数m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据条件,求下列曲线的方程.
(1)已知两定点![]() ,曲线上的点
,曲线上的点![]() 到
到![]() 距离之差的绝对值为
距离之差的绝对值为![]() ,求曲线的方程;
,求曲线的方程;
(2)在 ![]() 轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为
轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为![]() 的椭圆的标准方程.
的椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(![]() )能否出现
)能否出现![]() 的情况?说明理由.
的情况?说明理由.
(![]() )证明过
)证明过![]() ,
,![]() ,
,![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长为定值.
轴上截得的弦长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com