
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点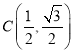 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心,半径为
为圆心,半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,
,![]() 为曲线
为曲线![]() 上的一动点.
上的一动点.
(I)求动点![]() 对应的参数从
对应的参数从![]() 变动到
变动到![]() 时,线段
时,线段![]() 所扫过的图形面积;
所扫过的图形面积;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 为线段
为线段![]() 的中点?若存在,求出点
的中点?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司代理销售某种品牌小商品,该产品进价为5元/件,销售时还需交纳品牌使用费3元/件,售价为![]() 元/件,其中
元/件,其中![]() ,且
,且![]() .根据市场调查,当
.根据市场调查,当![]() ,且
,且![]() 时,每月的销售量
时,每月的销售量![]() (万件)与
(万件)与![]() 成正比;当
成正比;当![]() ,且
,且![]() 时,每月的销售量
时,每月的销售量![]() (万件)与
(万件)与![]() 成反比.已知售价为15元/件时,月销售量为9万件.
成反比.已知售价为15元/件时,月销售量为9万件.
(1)求该公司的月利润![]() (万件)与每件产品的售价
(万件)与每件产品的售价![]() (元)的函数关系式;
(元)的函数关系式;
(2)当每件产品的售价为多少元时,该公司的月利润![]() 最大?并求出最大值.
最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | |
直径/mm | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):①
表示相应事件的概率):①![]() ;②
;②![]() ;③
;③![]() .判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备
.判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”,将直径尺寸在
之外的零件认定为是“次品”,将直径尺寸在![]() 之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.
之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() 是边长为
是边长为![]() 的正三角形,直线
的正三角形,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
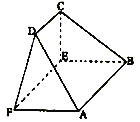
(I)求证:![]() ;
;
(Ⅱ)若![]() ,四边形
,四边形![]() 为平行四边形,求平面
为平行四边形,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家大约在公元222年赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)类比“赵爽弦图”,赵爽弦图可类似地构造如图所示的图形,它是由个3全等的等边三角形与中间的一个小等边三角形组成的一个大等边三角形,设DF2AF,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,利用斜二侧画法得到水平放置的![]() 的直观图
的直观图![]() ,其中
,其中![]() 轴,
轴,![]() 轴.若
轴.若![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,记
,记![]() ,执行如图②的框图,则输出
,执行如图②的框图,则输出![]() 的值
的值
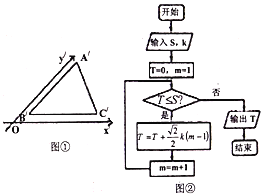
A. 12B. 10C. 9D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂![]() ,
,![]() 两条生产线生产同款产品,若产品按照一、二、三等级分类,则每件可分别获利10元、8元、6元,现从
两条生产线生产同款产品,若产品按照一、二、三等级分类,则每件可分别获利10元、8元、6元,现从![]() ,
,![]() 生产线的产品中各随机抽取100件进行检测,结果统计如下图:
生产线的产品中各随机抽取100件进行检测,结果统计如下图:
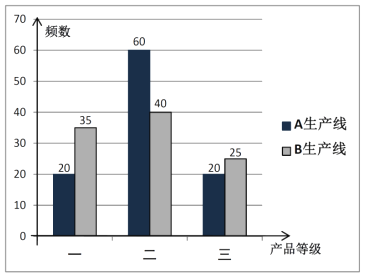
(1)根据已知数据,判断是否有99%的把握认为一等级产品与生产线有关?
(2)分别计算两条生产线抽样产品获利的方差,以此作为判断依据,说明哪条生产线的获利更稳定?
(3)估计该厂产量为2000件产品时的利润以及一等级产品的利润.
附:![]()
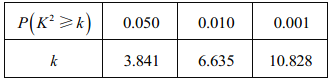
查看答案和解析>>
科目:高中数学 来源: 题型:
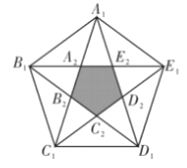
【题目】中华人民共和国国旗是五星红旗,旗面左上方缀着的五颗黄色五角星,四颗小五角星环拱于大星之右,象征中国共产党领导下的革命人民大团结和人民对党的衷心拥护.五角星可通过正五边形连接对角线得到,且它具有一些优美的特征,如![]() 且等于黄金分割比
且等于黄金分割比![]() ,现从正五边形A1B1C1D1E1内随机取一点,则此点取自正五边形A2B2C2D2E2内部的概率为()
,现从正五边形A1B1C1D1E1内随机取一点,则此点取自正五边形A2B2C2D2E2内部的概率为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com