
【题目】己知函数f(x)=loga(3x+1),g(x)=loga(1﹣3x),(a>0且a≠1).
(1)求函数F(x)=f(x)﹣g(x)的定义域;
(2)判断F(x)=f(x)﹣g(x)的奇偶性,并说明理由4;
(3)确定x为何值时,有f(x)﹣g(x)>0.
【答案】
(1)
解:F(x)=f(x)﹣g(x)=loga(3x+1)﹣loga(1﹣3x),
∴ ![]() ,解得
,解得 ![]() .
.
∴F(x)=f(x)﹣g(x)的定义域是(﹣ ![]() ,
, ![]() )
)
(2)
解:由(1)知F(x)定义域关于原点对称,
∵F(x)=loga(3x+1)﹣loga(1﹣3x),
F(﹣x)=loga(﹣3x+1)﹣loga(1+3x)=﹣F(x).
∴F(x)=f(x)﹣g(x)是奇函数
(3)
解:∵f(x)﹣g(x)>0,
∴f(x)>g(x),
即 loga(3x+1)>loga(1﹣3x),
① 当a>1时, 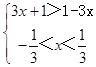 ,解得 0<x<
,解得 0<x< ![]() .
.
②当0<a<1时, 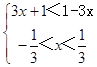 ,解得﹣
,解得﹣ ![]() .
.
综上所述:当a>1时,f(x)﹣g(x)>0的解是0<x< ![]() .
.
当0<a<1时,f(x)﹣g(x)>0的解是﹣ ![]()
【解析】(1)由真数大于零即可列出方程组 ![]() ,解出即可;(2)由F(﹣x)=loga(﹣3x+1)﹣loga(1+3x)=﹣F(x),再结合定义域即能得出答案.(3)不等式f(x)﹣g(x)>0转化为loga(3x+1)>loga(1﹣3x),然后分当a>1时和0<a<1两种情况进行讨论,利用对数函数的单调性列出方程组即得答案.
,解出即可;(2)由F(﹣x)=loga(﹣3x+1)﹣loga(1+3x)=﹣F(x),再结合定义域即能得出答案.(3)不等式f(x)﹣g(x)>0转化为loga(3x+1)>loga(1﹣3x),然后分当a>1时和0<a<1两种情况进行讨论,利用对数函数的单调性列出方程组即得答案.
【考点精析】掌握对数函数的定义域是解答本题的根本,需要知道对数函数的定义域范围:(0,+∞).


科目:高中数学 来源: 题型:
【题目】某商场举行节日促销活动,消费满一定数额即可获得一次抽奖机会,抽奖这可以从以下两种方式中任选一种进行抽奖.
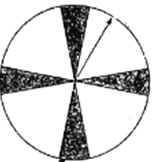
抽奖方式①:让抽奖者随意转动如图所示的圆盘,圆盘停止后指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即中奖.
,边界忽略不计)即中奖.
抽奖方式②:让抽奖者从装有3个白球和3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即中奖.
假如你是抽奖者,为了让中奖的可能性大,你应该选择哪一种抽奖方式?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:(1)函数f(x)在[0,+∞)上是增函数,在(﹣∞,0)上也是增函数,所以f(x)在R上是增函数;(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0,且a>0; (3)y=x2﹣2|x|﹣3的递增区间为[1,+∞);(4)函数y=lg10x和函数y=elnx表示相同函数.其中正确命题的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,记函数f(x)=a ![]() +
+ ![]() +
+ ![]() 的最大值为g(a).
的最大值为g(a).
(1)设t= ![]() +
+ ![]() ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);
(2)求g(a);
(3)试求满足g(a)=g( ![]() )的所有实数a.
)的所有实数a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四种说法: ①函数y=ax(a>0且a≠1)与函数y=logaax(a>0且a≠1)的定义域相同;
②函数y=x3与y=3x的值域相同;
③函数y= ![]() +
+ ![]() 与y=
与y= ![]() 都是奇函数;
都是奇函数;
④函数y=(x﹣1)2与y=2x﹣1在区间[0,+∞)上都是增函数.
其中正确的序号是(把你认为正确叙述的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,
, ![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() ,
, ![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() 恰为数列
恰为数列![]() 中的一项?若存在,求所有满足要求的
中的一项?若存在,求所有满足要求的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com