练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    直线x＝t过双曲线(a＞0，b＞0)的右焦点且与双曲线的两条渐近线分别交于A，B两点，若原点在以AB为直径的圆外，则双曲线离心率的取值范围是

    [　　]

    A．(1，＋∞)

    B．(1，)

    C．(1，)

    D．(1，1＋)

    答案：C
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：天利38套《2008全国各省市高考模拟试题汇编　精华大字版》、数学理 题型：044

    若F1、F2分别为双曲线的左、右焦点，O为坐标原点，E在双曲线的左支上，点M在右准线上，且满足(λ＞0)．

    (Ⅰ)求此双曲线的离心率；

    (Ⅱ)若此双曲线过点()，直线l过其右焦点且与右支交于P、Q两点，若线段PQ的中点R在直线x＝t(t≤1)上的射影C满足PC⊥QC，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：江西省高安中学2012届高三第三次模拟考试数学文科试题 题型：044

    已知椭圆＋＝1(a＞b＞0)长轴上有一倾点到两个焦点之间的距离分别为：3＋2，3－2

    (1)求椭圆的方程；

    (2)如果直线x＝t(teR)与椭圆相交于A，B，若C(－3，0)，D(3，0)，证明直线CA与直线BD的交点K必在一条确定的双曲线上；

    (3)过点Q(1，0)作直线l(与x轴不垂直)与椭圆交于M，N两点，与y轴交于点R，、若＝λ，＝μ，求证：λ＋μ为定值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江西省、临川一中高三8月联考理科数学试卷（解析版） 题型：解答题

    设双曲线C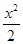：－y2＝1的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q．

    （1）若直线m与x轴正半轴的交点为T，且·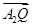＝1，求点T的坐标；

    （2）求直线A1P与直线A2Q的交点M的轨迹E的方程；

    （3）过点F（1，0）作直线l与（2）中的轨迹E交于不同的两点A、B，设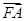＝λ·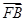，若λ∈[－2，－1]，求|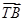＋|（T为（1）中的点）的取值范围．

     

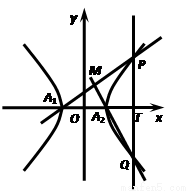
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    22.已知倾斜角为45°的直线l过点A(1,－2)和点B,B在第一象限,|AB|＝3.

    (1)求点B的坐标;

    (2)若直线l与双曲线C:－y2＝1(a>0)相交于E、F两点,且线段EF的 中点坐标为(4,1),求a的值；

    (3)对于平面上任一点P,当点Q在线段AB上运动时,称|PQ|的最小值为P 与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的 距离h关于t的函数关系式.

    查看答案和解析>>

    同步练习册答案