Question

【题目】如图，在四棱锥E﹣ABCD中，底面ABCD为矩形，平面ABCD⊥平面ABE，∠AEB=90°，BE=BC，F为CE的中点，
（1）求证：AE∥平面BDF；
（2）求证：平面BDF⊥平面ACE；
（3）2AE=EB，在线段AE上找一点P，使得二面角P﹣DB﹣F的余弦值为 ， 求AP的长．

Answer 1

【答案】证明：（1）设AC∩BD=G，连接FG，易知G是AC的中点，
∵F是EC中点．
∴在△ACE中，FG∥AE，
∵AE平面BFD，FG平面BFD，
∴AE∥平面BFD．…（4分）
（2）∵平面ABCD⊥平面ABE，BC⊥AB，
平面ABCD∩平面ABE=AB，
∴BC⊥平面ABE，又∵AE平面ABE，
∴BC⊥AE，
又∵AE⊥BE，BC∩BE=B，
∴AE⊥平面BCE，即AE⊥BF，
在△BCE中，BE=CB，F为CE的中点，
∴BF⊥CE，AE∩CE=E，
∴BF⊥平面ACE，
又BF平面BDF，
∴平面BDF⊥平面ACE．
（3）如图建立坐标系，设AE=1，
则B（2，0，0），D（0，1，2），C（2，0，2），F（1，0，1），
设P（0，a，0），=(-2,1,2)，=(-1,0,1)，=(2,-a,0)
设⊥面BDF，且=(x1,y1,z1)
则由⊥得﹣2x1+y1+2z1=0，
由⊥得﹣x1+z1=0，
令z1=1得x1=1，y1=0，从而=(1,0,1)
设⊥面BDP，且=(x2,y2,z2)，则
由⊥得﹣2x2+y2+2z2=0，
由⊥得2x2﹣ay2=0，
令y2=2得x2=a，z2=a﹣1，从而=(a,2,a-1)
==
解得a=0或a=1（舍）
即P在E处．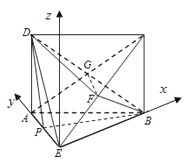

【解析】（1）根据线面平行的判定定理即可证明AE∥平面BDF；
（2）根据面面垂直的判定定理即可证明平面BDF⊥平面ACE；
（3）建立空间坐标系，求出平面的法向量，利用向量法即可得到结论．
【考点精析】认真审题，首先需要了解平面与平面垂直的判定(一个面过另一个平面的垂线，则这两个平面垂直)．