
| A. | (1,2) | B. | (2,+∞) | C. | $(1,\;\sqrt{2})$ | D. | $(\sqrt{2},\;+∞)$ |
分析 不妨设F1(0,c),F2(0,-c),则过F1与渐近线$y=\frac{a}{b}x$平行的直线为$y=\frac{a}{b}x+c$,联立直线组成方程组,求出M坐标,利用点与圆的位置关系,列出不等式然后求解离心率即可.
解答 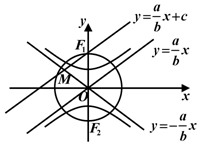 解:如图1,不妨设F1(0,c),F2(0,-c),则过F1与渐近线$y=\frac{a}{b}x$平行的直线为$y=\frac{a}{b}x+c$,
解:如图1,不妨设F1(0,c),F2(0,-c),则过F1与渐近线$y=\frac{a}{b}x$平行的直线为$y=\frac{a}{b}x+c$,
联立$\left\{\begin{array}{l}y=\frac{a}{b}x+c\\ y=-\frac{a}{b}x\end{array}\right.$解得$\left\{\begin{array}{l}x=-\frac{bc}{2a}\\ y=\frac{c}{2}\end{array}\right.$即$M(-\frac{bc}{2a},\frac{c}{2})$
因M在以线段F1F2为直径的圆x2+y2=c2内,
故${(-\frac{bc}{2a})^2}+{(\frac{c}{2})^2}<{c^2}$,化简得b2<3a2,
即c2-a2<3a2,解得$\frac{c}{a}<2$,又双曲线离心率$e=\frac{c}{a}>1$,所以双曲线离心率的取值范围是(1,2).
故选:A.
点评 本题考查直线与双曲线的位置关系的应用,双曲线的简单性质的应用,考查数形结合以及计算能力.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
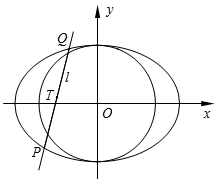 在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.
在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
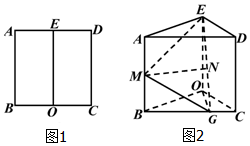 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
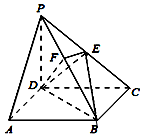 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,EF⊥PB交PB于点F.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com