
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
分析 (Ⅰ)求出回归系数,即可求出利润额y对销售额x的回归直线方程$\widehaty=\widehatbx+\widehata$;
(Ⅱ)x=4代入,即可得出结论.
解答 解:(Ⅰ)设回归直线的方程是:$\widehaty=bx+a$,$\overline y=3.4,\overline x=6$,
∴$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$=$\frac{4.2+0.4+0.6+4.8}{9+1+1+9}$=0.5,$\widehata=\overline y-\widehatb\overline x$=0.4,
∴y对销售额x的回归直线方程为:$\stackrel{∧}{y}$=0.5x+0.4;------(8分)
(Ⅱ)当销售额为4(千万元)时,利润额为:$\stackrel{∧}{y}$=0.5×4+0.4=2.4(千万元).---(12分)
点评 本题考查回归方程及运用,考查学生的计算能力,正确计算是关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
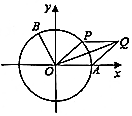 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>4} | B. | {x|x<-2或x>2} | C. | {x|x<0或x>4} | D. | {x|x<0或x>6} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 零件数x(个) | 18 | 20 | 22 |
| 加工时间y(分钟) | 27 | 30 | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-1 | B. | y-1=$\frac{\sqrt{2}}{2}$(x+2) | C. | $\frac{x}{5}$+$\frac{y}{5}$=1 | D. | $\sqrt{2}$x+2y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | b<a<c | C. | c<a<b | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com