
 ;(2)f(x)的单调递增区间是(kπ-
;(2)f(x)的单调递增区间是(kπ-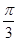 ,kπ+),k∈Z;f(x)的单调递减区间是(kπ+,kπ+
,kπ+),k∈Z;f(x)的单调递减区间是(kπ+,kπ+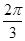 ),k∈Z;函数f(x)的对称轴为
),k∈Z;函数f(x)的对称轴为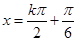 ,k∈Z;函数f(x)的对称中心为
,k∈Z;函数f(x)的对称中心为 ,k∈Z .
,k∈Z .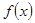 的解析式,化为标准式,然后利用周期公式
的解析式,化为标准式,然后利用周期公式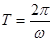 来求;(2) 根据正弦曲线的单调区间:
来求;(2) 根据正弦曲线的单调区间: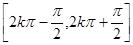 单调递增,
单调递增,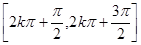 单调递减求目标函数的单调区间,对称轴是根据
单调递减求目标函数的单调区间,对称轴是根据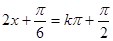 来求;对称中心是根据
来求;对称中心是根据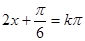 来求.
来求.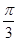 ,kπ+),k∈Z, 8分
,kπ+),k∈Z, 8分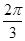 ),k∈Z. 10分
),k∈Z. 10分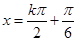 ,k∈Z, 12分
,k∈Z, 12分 ,k∈Z 14分
,k∈Z 14分

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com