
【题目】设全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
【答案】
(1)解:由集合B中的不等式2x﹣4≥x﹣2,解得x≥2,
∴B={x|x≥2},又A={x|﹣1≤x<3},
∴A∩B={x|2≤x<3},又全集U=R,
∴U(A∩B)={x|x<2或x≥3}
(2)解:由集合C中的不等式2x+a>0,解得x>﹣ ![]() ,
,
∴C={x|x>﹣ ![]() },
},
∵B∪C=C,
∴BC,
∴﹣ ![]() <2,解得a>﹣4;
<2,解得a>﹣4;
故a的取值范围为(﹣4,+∞)
【解析】(1)求出集合B中不等式的解集确定出集合B,求出集合A与集合B的公共解集即为两集合的交集,根据全集为R,求出交集的补集即可;(2)求出集合C中的不等式的解集,确定出集合C,由B与C的并集为集合C,得到集合B为集合C的子集,即集合B包含于集合C,从而列出关于a的不等式,求出不等式的解集即可得到a的范围.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() =(2cos
=(2cos![]() ,
, ![]() sin
sin![]() ),
),![]() =(cos
=(cos![]() ,2cos
,2cos![]() ),(ω>0),设函数f(x)=
),(ω>0),设函数f(x)=![]()
![]() ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求函数f(x)的表达式;
(2)求f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.

附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
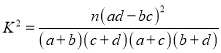
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现如今网上购物已经习以为常,变成人们日常生活的一部分,冲击着人们的传统消费习惯、思维和生活方式,以其特殊的优势而逐渐深入人心.某市场调研机构对在“双十一”购物的![]() 名年龄在
名年龄在![]() 岁的消费者进行了年龄段和性别分布的调查,其部分结果统计如下表:
岁的消费者进行了年龄段和性别分布的调查,其部分结果统计如下表:
年龄(岁) |
|
|
|
|
|
女 | 70 | 50 | 40 | 30 | 20 |
男 | 30 |
| 20 | 15 | 10 |
(1)若按年龄用分层抽样的方法抽取84个人,其中在![]() 内抽取了36人,求
内抽取了36人,求![]() 的值.
的值.
(2)在(1)的条件下,用分层抽样的方法在![]() 岁的消费者中抽取一个容量为8的本,将该样本看成一个总体,从中任取3人,记
岁的消费者中抽取一个容量为8的本,将该样本看成一个总体,从中任取3人,记![]() 表示抽得女性消费者的人数,求随机变量
表示抽得女性消费者的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,四边形
中,四边形![]() 与四边形
与四边形![]() 均为边长为2的正方形,
均为边长为2的正方形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
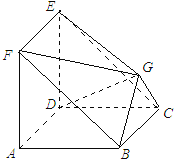
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
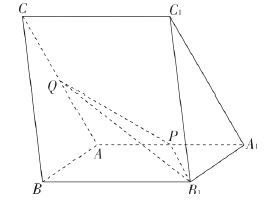
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() 恒等于常数
恒等于常数![]() ,则称
,则称![]() 具有局部等差数列
具有局部等差数列![]() .
.
(1)若![]() 具有局部等差数列
具有局部等差数列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有局部等差数列
是否具有局部等差数列![]() ,并说明理由;
,并说明理由;
(3)设![]() 既具有局部等差数列
既具有局部等差数列![]() ,又具有局部等差数列
,又具有局部等差数列![]() ,求证:
,求证:![]() 具有局部等差数列
具有局部等差数列![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com