【题目】已知函数f(x)＝x－1＋
x2－2，试利用基本初等函数的图象，判断f(x)有几个零点，并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1)．
【答案】3个零点分别在区间(－3，－2)，
，(1,2)内．
【解析】试题分析：本题是一个比较复杂的函数求零点的问题，通过转化为两个较熟悉的函数研究.容易得到两个数有三个交点，所以有三个零点.零点的范围不好确定，本题很巧妙地应用了零点定理，求出了个的范围.这种方法值得好好体会.
试题解析：由f(x)=0，得
，令
，
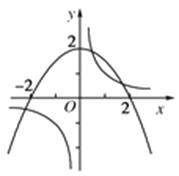
.分别画出它们的图象如图，其中抛物线的顶点坐标为(0,2)，与x轴的交点为(-2,0)、(2,0)，
与
的图象有3个交点，从而函数f(x)有3个零点．由f(x)的解析式知x≠0，f(x)的图象在(-∞，0)和(0，+∞)上分别是连续不断地曲线，且
即
，
.所以三个零点分别在区间（-3，-2），，（1,2）内.
全程金卷系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
（a＞b＞0）的离心率为
，以原点O为圆心，椭圆的短半轴长为半径的圆与直线x﹣y+
=0相切．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线l：y=kx+m与椭圆C相交于A、B两点，且kOAkOB=﹣
，判断△AOB的面积是否为定值？若为定值，求出定值；若不为定值，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学（理）】已知函数
，其中常数
.
（Ⅰ）讨论
在
上的单调性；
（Ⅱ）当
时，若曲线
上总存在相异两点
，使曲线在
两点处的切线互相平行，试求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中,根据下列条件解三角形,其中有两个解的是（ ）
A. b="10," A=450, C=600 B. a=6, c=5, B=600
C. a=7, b=5, A=600 D. a=14, b="16," A=450
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于函数
有下列命题：
①函数
的图象关于
轴对称；
②在区间
上，函数
是减函数；
③在区间
上，函数
是增函数；
④函数
的值域是
.其中正确命题序号为____.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
为实数.
（1）若关于
的不等式
的解集为
，求实数
的值；
（2）设
，当
时，求函数
的最小值（用
表示）；
（3）若关于
不等式
的解集中恰好有两个整数解，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（1）求证： 
.
（2）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：
sin213°＋cos217°－sin13°cos17°；
sin215°＋cos215°－sin15°cos15°；
sin218°＋cos212°－sin18°cos12°；
sin2(－18°)＋cos248°－sin(－18°)cos48°；
sin2(－25°)＋cos255°－sin(－25°)cos55°.
①试从上述五个式子中选择一个，求出这个常数；
②根据①的计算结果，将该同学的发现推广为三角恒等式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
