
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 平面
平面![]() .
.
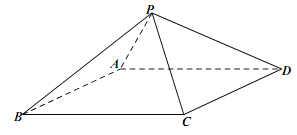
(1)证明:![]() ;
;
(2)若平面![]() 平面
平面![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)2
【解析】
(1)由底面ABCD是平行四边形,得CD//AB, 可得CD//平面PAB,结合平面PAB∩平面PCD=l,得到CD//l, 由平行公理可得![]() ;
;
(2)连接AC, BD交于点O,则O是AC, BD的中点,证明PO⊥平面ABCD,再解三角形求得PO与底面积,则四棱锥![]() 的体积可求.
的体积可求.
(1)因为底面![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵平面![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() .
.
(2)连接![]() ,
,![]() 交于点
交于点![]() ,则点
,则点![]() 是
是![]() ,
,![]() 的中点,
的中点,
连接![]() .∵
.∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,又
,又![]() ,
,
∴![]() 底面
底面![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连
,连![]() 并延长交
并延长交![]() 于
于![]() ,连
,连![]() ,
,
则![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() ,∴
,∴![]() ,
,
![]() 为平面
为平面![]() 与平面
与平面![]() 的平面角,
的平面角,
![]() 平面
平面![]() 平面
平面![]()
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
所以四棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知过点![]() 的直线l:
的直线l:![]() 与抛物线E:
与抛物线E:![]() (
(![]() )交于B,C两点,且A为线段
)交于B,C两点,且A为线段![]() 的中点.
的中点.
(1)求抛物线E的方程;
(2)已知直线![]() :
:![]() 与直线l平行,过直线
与直线l平行,过直线![]() 上任意一点P作抛物线E的两条切线,切点分别为M,N,是否存在这样的实数m,使得直线
上任意一点P作抛物线E的两条切线,切点分别为M,N,是否存在这样的实数m,使得直线![]() 恒过定点A?若存在,求出m的值;若不存在,说明理由.
恒过定点A?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的棱长均为6,其内有
的棱长均为6,其内有![]() 个小球,球
个小球,球![]() 与三棱锥
与三棱锥![]() 的四个面都相切,球
的四个面都相切,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切,如此类推,…,球
都相切,如此类推,…,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),则球
),则球![]() 的体积等于__________,球
的体积等于__________,球![]() 的表面积等于__________.
的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为![]() .在以原点O为极点,x轴正半轴为极轴的极坐标系中,P的极坐标为
.在以原点O为极点,x轴正半轴为极轴的极坐标系中,P的极坐标为![]() ,直线l过点P.
,直线l过点P.
(1)若直线l与OP垂直,求直线l的直角标方程:
(2)若直线l与曲线C交于A,B两点,且![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
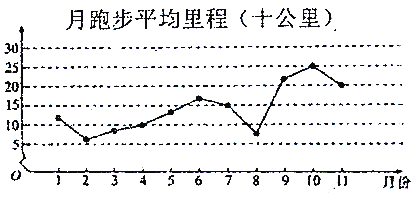
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈(![]() ,
,![]() ),则输入的n的值为( )
),则输入的n的值为( )
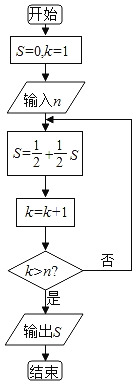
A.7B.6C.5D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com