
求棱长为a的正方体ABCD-A1B1C1D1的面对角线A1C1与AB1的距离.
|
解法一:连结BD1,取A1B1的中点E,连BE交AB1于M,连D1E交A1C1于N,连MN.
因为ΔA1NE∽ΔC1ND1,所以 则 ∵ 由三垂线定理知BD1与A1C1、AB1都垂直,故MN为两对角线的公垂线, 又ΔEMN∽ΔEBD1 故 解法二:取A1M=
解法三:可转化为求平行平面间的距离.连A1D,C1D,A1C1,B1C.易知A1D∥B1C,A1C1∥AC.故平面A1DC1∥平面AB1C.连BD1,设与平面A1DC1交于M,与平面AB1C交于N.因BD1与图中所示6条面对角线都垂直,故BD⊥面A1DC1,也垂直于AB1C.即MN是A1C1与AB1的距离,在RtΔD1DB中,D1M=
MN= 说明:上例还可以利用直线与平面平行、体积转换等方法求解. |


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
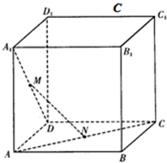 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.查看答案和解析>>
科目:高中数学 来源: 题型:
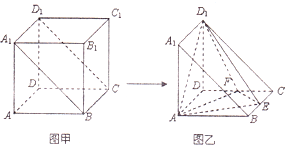 将棱长为a的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点E,F分别是BC,DC的中点.
将棱长为a的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点E,F分别是BC,DC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com