
【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:
(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注: ![]()
【答案】
(1)解:在满意产品的女用户中应抽取20× ![]() =2(人)记r,s
=2(人)记r,s
在满意产品的男用户中应抽取30× ![]() =3(人)记a,b,c
=3(人)记a,b,c
从5人中任选2人,共有10种情况:ab,ac,ar,as,bc,br,bs,cr,cs,rs
其中一男一女的情况6种,所以P= ![]() =
= ![]()
(2)解:K2= ![]() ≈5.333>5.024
≈5.333>5.024
所以有97.5%的把握认为用户对该产品是否满意与用户性别有关
【解析】(1)根据分层抽样原理,计算应抽取的女生、男生人数,用列举法计算出基本事件的个数进而得出所求事件的概率。(2)计算出K2 的值,再对照临界值即可得出结论。
【考点精析】认真审题,首先需要了解分层抽样(先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本).


科目:高中数学 来源: 题型:
【题目】设![]() 是异面直线,则以下四个命题:①存在分别经过直线
是异面直线,则以下四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;②存在分别经过直线
的两个互相垂直的平面;②存在分别经过直线![]() 和
和![]() 的两个平行平面;③经过直线
的两个平行平面;③经过直线![]() 有且只有一个平面垂直于直线
有且只有一个平面垂直于直线![]() ;④经过直线
;④经过直线![]() 有且只有一个平面平行于直线
有且只有一个平面平行于直线![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电商中“猫狗大战”在节日期间的竞争异常激烈,在刚过去的618全民年中购物节中,某东当日交易额达1195亿元,现从该电商“剁手党”中随机抽取100名顾客进行回访,按顾客的年龄分成了6组,得到如下所示的频率直方图. 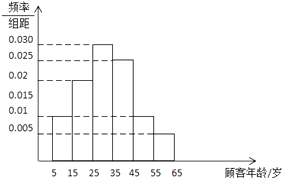
(1)求顾客年龄的众数,中位数,平均数(每一组数据用中点做代表);
(2)用样本数据的频率估计总体分布中的概率,则从全部顾客中任取3人,记随机变量X为顾客中年龄小于25岁的人数,求随机变量X的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函数f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值时x取值集合;
(3)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从6名学生会干部(其中男生4人,女生2人)中选3人参加青年联合会志愿者。
(1)设所选3人中女生人数为 ![]() ,求
,求 ![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系 ![]() 中,过椭圆
中,过椭圆 ![]() :
: ![]() (
( ![]() )右焦点的直线
)右焦点的直线 ![]() 交
交 ![]() 于
于 ![]() ,
, ![]() 两点,
两点, ![]() 为
为 ![]() 的中点,且
的中点,且 ![]() 的斜率为
的斜率为 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ) ![]() ,
, ![]() 为
为 ![]() 上的两点,若四边形
上的两点,若四边形 ![]() . 的对角线
. 的对角线 ![]() ,求四边形
,求四边形 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由![]() 沿棱柱侧面经过棱
沿棱柱侧面经过棱![]() 到点
到点![]() 的最短路线长为
的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为
的交点为![]() .
.

(1)求三棱柱![]() 的体积;
的体积;
(2)证明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数, ![]() 为常数.
为常数.
(1)确定![]() 的值;
的值;
(2)求证: ![]() 是
是![]() 上的增函数;
上的增函数;
(3)若对于区间![]() 上的每一个
上的每一个![]() 值,不等式
值,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com