
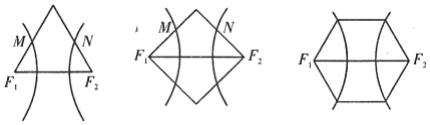
【题目】下列三图中的多边形均为正多边形,![]() ,
,![]() 是所在边的中点,双曲线均以图中的
是所在边的中点,双曲线均以图中的![]() ,
,![]() 为焦点,设图示①②③中的双曲线的离心率分别为
为焦点,设图示①②③中的双曲线的离心率分别为![]() ,
,![]() ,
,![]() 、则
、则![]() ,
,![]() ,
,![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过20克的为合格.
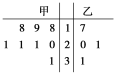
(1)从甲、乙两车间分别随机抽取2个零件,求甲车间至少一个零件合格且乙车间至少一个零件合格的概率;
(2)质检部门从甲车间8个零件中随机抽取3个零件进行检测,已知三件中有两件是合格品的条件下,另外一件是不合格品的概率.
(3)若从甲、乙两车间12个零件中随机抽取2个零件,用![]() 表示乙车间的零件个数,求X的分布列与数学期望.
表示乙车间的零件个数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,O为坐标原点,点![]() ,
,![]() ,Q为平面上的动点,且
,Q为平面上的动点,且![]() ,线段
,线段![]() 的中垂线与线段
的中垂线与线段![]() 交于点P.
交于点P.
![]() 求
求![]() 的值,并求动点P的轨迹E的方程;
的值,并求动点P的轨迹E的方程;
![]() 若直线l与曲线E相交于A,B两点,且存在点
若直线l与曲线E相交于A,B两点,且存在点![]() 其中A,B,D不共线
其中A,B,D不共线![]() ,使得
,使得![]() ,证明:直线l过定点.
,证明:直线l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
A. 众数 B. 平均数 C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,小明为了帮助爸爸戒烟,在爸爸包里放一个小盒子,里面随机摆放三支香烟和三支跟香烟外形完全一样的“戒烟口香糖”,并且和爸爸约定,每次想吸烟时,从盒子里任取一支,若取到口香糖则吃一支口香糖,不吸烟;若取到香烟,则吸一支烟,不吃口香糖,假设每次香烟和口香糖被取到的可能性相同,则“口香糖吃完时还剩2支香烟”的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,
, ![]() ,动点
,动点![]() 满足
满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 有且仅有一个公共点
有且仅有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,求证:以
,求证:以![]() 为直径的圆过定点
为直径的圆过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 与
与![]() 、
、![]() 两点连线的斜率之积为
两点连线的斜率之积为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() (其中
(其中![]() 为坐标原点),求
为坐标原点),求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com