
【题目】设f(x)=ln(x+1)+ ![]() +ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=
+ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y= ![]() x在(0,0)点相切.
x在(0,0)点相切.
(1)求a,b的值;
(2)证明:当0<x<2时,f(x)< ![]() .
.
【答案】
(1)
解:由y=f(x)过(0,0),∴f(0)=0,∴b=﹣1
∵曲线y=f(x)与直线y= ![]() x在(0,0)点相切.
x在(0,0)点相切.
∴y′|x=0= ![]()
∴a=0;
(2)
证明:由(1)知f(x)=ln(x+1)+ ![]() -1
-1
由均值不等式,当x>0时, ![]() ,∴
,∴ ![]() ①
①
令k(x)=ln(x+1)﹣x,则k(0)=0,k′(x)= ![]() ,∴k(x)<0
,∴k(x)<0
∴ln(x+1)<x,②
由①②得,当x>0时,f(x)< ![]() x
x
记h(x)=(x+6)f(x)﹣9x,则当0<x<2时,h′(x)=f(x)+(x+6)f′(x)﹣9
< ![]() <
< ![]()
= ![]()
∴h(x)在(0,2)内单调递减,又h(0)=0,∴h(x)<0
∴当0<x<2时,f(x)< ![]()
【解析】(1)由y=f(x)过(0,0),可求b的值,根据曲线y=f(x)与直线y= ![]() x在(0,0)点相切,利用导函数,可求a的值;(2)由(1)知f(x)=ln(x+1)+
x在(0,0)点相切,利用导函数,可求a的值;(2)由(1)知f(x)=ln(x+1)+ ![]() -1,由均值不等式,可得
-1,由均值不等式,可得 ![]() ,构造函数k(x)=ln(x+1)﹣x,可得ln(x+1)<x,从而当x>0时,f(x)<
,构造函数k(x)=ln(x+1)﹣x,可得ln(x+1)<x,从而当x>0时,f(x)< ![]() x,记h(x)=(x+6)f(x)﹣9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证
x,记h(x)=(x+6)f(x)﹣9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】某生产企业研发了一种新产品,该产品在试销一个阶段后得到销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:万件)之间的一组数据,如下表所示:
(单位:万件)之间的一组数据,如下表所示:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)从反馈的信息来看,消费者对该产品的心理价(单位:元/件)在![]() 内,已知该产品的成本是
内,已知该产品的成本是![]() 元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
参考数据:![]()
参考公式: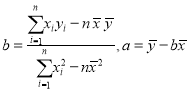
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,记M的轨迹为曲线C.
,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过坐标原点O的直线l交C于P、Q两点,点P在第一象限,![]() 轴,垂足为H.连结QH并延长交C于点R.
轴,垂足为H.连结QH并延长交C于点R.
(i)设O到直线QH的距离为d.求d的取值范围;
(ii)求![]() 面积的最大值及此时直线l的方程.
面积的最大值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在充分竞争的市场环境中,产品的定价至关重要,它将影响产品的销量,进而影响生产成本、品牌形象等![]() 某公司根据多年的市场经验,总结得到了其生产的产品A在一个销售季度的销量
某公司根据多年的市场经验,总结得到了其生产的产品A在一个销售季度的销量![]() 单位:万件
单位:万件![]() 与售价
与售价![]() 单位:元
单位:元![]() 之间满足函数关系
之间满足函数关系 ,A的单件成本
,A的单件成本![]() 单位:元
单位:元![]() 与销量y之间满足函数关系
与销量y之间满足函数关系![]() .
.
![]() 当产品A的售价在什么范围内时,能使得其销量不低于5万件?
当产品A的售价在什么范围内时,能使得其销量不低于5万件?
![]() 当产品A的售价为多少时,总利润最大?
当产品A的售价为多少时,总利润最大?![]() 注:总利润
注:总利润![]() 销量
销量![]() 售价
售价![]() 单件成本
单件成本![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种机器零件转速在符合要求的范围内使用时间随机器运转速度的变化而变化,某检测员随机收集了20个机器零件的使用时间与转速的数据,列表如下:
机器转速(转/分) | 189 | 193 | 190 | 185 | 183 | 202 | 187 | 203 | 192 | 201 |
零件使用时间(月) | 43 | 33 | 39 | 37 | 38 | 37 | 38 | 35 | 38 | 35 |
机器转速(转/分) | 193 | 197 | 191 | 186 | 191 | 188 | 185 | 204 | 201 | 189 |
零件使用时间(月) | 37 | 40 | 41 | 37 | 35 | 37 | 42 | 36 | 34 | 40 |
(Ⅰ)若“转速大于200转/分”为“高速”,“转速不大于200转/分”为“非高速”,“使用时间大于36个月”的为“长寿命”,“使用时间不大于36个月”的为“非长寿命”,请根据上表数据完成下面的![]() 列联表:
列联表:
高速 | 非高速 | 合计 | |
长寿命 | |||
非长寿命 | |||
合计 |
(Ⅱ)根据(Ⅰ)中的![]() 列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数![]() (千人)与时间
(千人)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() ),人均消费
),人均消费![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]()
(1)求该商场的日收益![]() (千元)与时间
(千元)与时间![]() (天)(
(天)(![]() ,
, ![]() )的函数关系式;
)的函数关系式;
(2)求该商场日收益的最小值(千元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月14日,“![]() 共享单车”终于来到芜湖,
共享单车”终于来到芜湖,![]() 共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于
共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的
,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的![]() 名市民,并根据这
名市民,并根据这![]() 名市民对该项目满意程度的评分(满分
名市民对该项目满意程度的评分(满分![]() 分),绘制了如下频率分布直方图:
分),绘制了如下频率分布直方图:

(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于![]() 分的市民中随机抽取
分的市民中随机抽取![]() 人进行座谈,求这
人进行座谈,求这![]() 人评分恰好都在
人评分恰好都在![]() 的概率;
的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数=![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线l1:y=m和l2:y= ![]() (m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2与函数y=|log2x|的图象从左至右相交于点C,D.记线段AC和BD在X轴上的投影长度分别为a,b,当m变化时,
(m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2与函数y=|log2x|的图象从左至右相交于点C,D.记线段AC和BD在X轴上的投影长度分别为a,b,当m变化时, ![]() 的最小值为( )
的最小值为( )
A.16 ![]()
B.8 ![]()
C.8 ![]()
D.4 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com