Question

17．如图所示，直线AB为圆O的切线，切点为B，点C在圆O上，∠ABC的平分线BE交圆O于点E，DB垂直BE交圆O于点D．
（1）证明：DB=DC；
（2）设圆O的半径为1，BC=$\sqrt{3}$，延长CE交AB于点F，求线段BF的长．

Answer 1

分析 （1）连接DE交BC于点G，由弦切角定理可得∠ABE=∠BCE，由已知角平分线可得∠ABE=∠CBE，于是得到∠CBE=∠BCE，BE=CE．由已知DB⊥BE，可知DE为⊙O的直径，Rt△DBE≌Rt△DCE，利用三角形全等的性质即可得到DC=DB．
（2）由（1）可知：DG是BC的垂直平分线，即可得到BG=$\frac{\sqrt{3}}{2}$．设DE的中点为O，连接BO，可得∠BOG=60°．从而∠ABE=∠BCE=∠CBE=30°．得到CF⊥BF．进而得到线段BF的长

解答 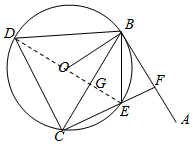（1）证明：连接DE交BC于点G，
由弦切角定理得，∠ABE=∠BCE．（1分）
∵∠ABE=∠CBE，∴∠CBE=∠BCE，BE=CE．（3分）
又∵DE⊥BE，∴DE是直径，∠DCE=90°．（4分）
∴△DBE≌△DCE，∴DC=DB．（5分）
（2）解：设DE与BC相交于点G，
由（1）知，∠CDE=∠BDE，DB=DC，故DG是BC的中垂线．（6分）
∵$BC=\sqrt{3}$，∴$BG=\frac{{\sqrt{3}}}{2}$．（7分）
连接BO，∵圆O的半径为1，∴∠BOG=60°，∠ABE=∠BCE=∠CBE=30°，
∴CF⊥BF．（9分），∴$BF=\frac{{\sqrt{3}}}{2}$．（10分）

点评 本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形全等等知识，需要较强的推理能力、分析问题和解决问题的能力．