
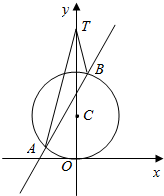
 如图,已知圆C的圆心在y轴的正半轴上,且与x轴相切,圆C与直线y=kx+3相交于A,B两点.当$k=\sqrt{3}$时,$|AB|=\sqrt{15}$.
如图,已知圆C的圆心在y轴的正半轴上,且与x轴相切,圆C与直线y=kx+3相交于A,B两点.当$k=\sqrt{3}$时,$|AB|=\sqrt{15}$.分析 (Ⅰ)设圆心C(0,b),b>0,则半径r=b,利用勾股定理,建立方程,即可求出b,从而求圆C的方程;
(Ⅱ)假设存在点T(0,t),联立方程组$\left\{\begin{array}{l}y=kx+3\\{x^2}+(y-2{)^2}=4\end{array}\right.$,利用韦达定理,结合kAT+kBT=0,即可得出结论.
解答  解:(Ⅰ)设圆心C(0,b),b>0,则半径r=b,…(2分)
解:(Ⅰ)设圆心C(0,b),b>0,则半径r=b,…(2分)
则圆心C(0,b)到$y=\sqrt{3}x+3$的距离$d=\frac{|3-b|}{2}$
∴$(\frac{|3-b|}{2}{)^2}+(\frac{{\sqrt{15}}}{2}{)^2}={b^2}$…(5分)
得∴b=2或b=-4(舍)
∴圆C的方程为∴x2+(y-2)2=4…(7分)
(Ⅱ)假设存在点T(0,t),设A(x1,y1),B(x2,y2)
联立方程组$\left\{\begin{array}{l}y=kx+3\\{x^2}+(y-2{)^2}=4\end{array}\right.$
得(1+k2)x2+2kx-3=0
则$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{2k}{{1+{k^2}}}\\{x_1}{x_2}=-\frac{3}{{1+{k^2}}}\end{array}\right.$…(10分)
由kAT+kBT=0
即$\frac{{{y_1}-t}}{x_1}+\frac{{{y_2}-t}}{x_2}=0$…(12分)
∴2kx1x2+(3-t)(x1+x2)=0,
∴6k+2k(3-t)=0对k取任意实数时都成立,∴t-3=3即t=6
故存在定点T(0,6),使得∠ATB始终被y轴平分.…(15分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查韦达定理的运用,属于中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (0.7)6<60.7<log0.76 | B. | ${({0.7})^6}<{log_{0.7}}6<{6^{0.7}}$ | ||
| C. | ${log_{0.7}}6<{({0.7})^6}<{6^{0.7}}$ | D. | ${log_{0.7}}6<{6^{0.7}}<{({0.7})^6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4) | B. | ($\frac{3}{5}$,$\frac{4}{5}$) | C. | ($\frac{3}{5}$,$\frac{4}{5}$)或(-$\frac{3}{5}$,-$\frac{4}{5}$) | D. | (1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com