
【题目】数列{an}满足a1=2,an+1=an2+6an+6(n∈N×)
(1)设Cn=log5(an+3),求证{Cn}是等比数列;
(2)求数列{an}的通项公式;
(3)设bn= ![]() ﹣
﹣ ![]() ,数列{bn}的前n项和为Tn , 求证:﹣
,数列{bn}的前n项和为Tn , 求证:﹣ ![]() ≤Tn<﹣
≤Tn<﹣ ![]() .
.
【答案】
(1)解:由an+1=an2+6an+6得an+1+3=(an+3)2,
∴ ![]() =2
=2 ![]() ,即cn+1=2cn
,即cn+1=2cn
∴{cn}是以2为公比的等比数列.
(2)解:又c1=log55=1,
∴cn=2n﹣1,即 ![]() =2n﹣1,
=2n﹣1,
∴an+3= ![]()
故an= ![]() ﹣3
﹣3
(3)解:∵bn= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,∴Tn=
,∴Tn= ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ﹣
﹣ ![]() .
.
又0< ![]()
![]() =
= ![]() .
.
∴﹣ ![]() ≤Tn<﹣
≤Tn<﹣ ![]()
【解析】(1)由已知可得,an+1+3=(an+3)2 , 利用构造法令Cn=log5(an+3),则可得 ![]() ,从而可证数列{cn}为等比数列;(2)由(1)可先求数列cn , 代入cn=log5(an+3)可求an;(3)把(2)中的结果代入整理可得,
,从而可证数列{cn}为等比数列;(2)由(1)可先求数列cn , 代入cn=log5(an+3)可求an;(3)把(2)中的结果代入整理可得, ![]() ,则代入Tn=b1+b2+…+bn相消可证
,则代入Tn=b1+b2+…+bn相消可证
【考点精析】关于本题考查的等比关系的确定和数列的前n项和,需要了解等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H. 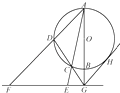
(1)求证:C,D,E,F四点共圆;
(2)若GH=8,GE=4,求EF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=4,BC=2,D是BC的中点,那么( ![]() ﹣
﹣ ![]() )
) ![]() =;若E是AB的中点,P是△ABC(包括边界)内任一点.则
=;若E是AB的中点,P是△ABC(包括边界)内任一点.则 ![]() 的取值范围是
的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin xcos x+cos2x+a;则f(x)的最小正周期为 , 若f(x)在区间[﹣
sin xcos x+cos2x+a;则f(x)的最小正周期为 , 若f(x)在区间[﹣ ![]() ,
, ![]() ]上的最大值与最小值的和为
]上的最大值与最小值的和为 ![]() ,则实数a的值为 .
,则实数a的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,设
,设![]() 表示数列
表示数列![]() 前
前![]() 项
项![]() ,
, ![]() ,
, ![]() ,
, ![]() 中的最大项.数列
中的最大项.数列![]() 满足:
满足: ![]() .
.
(![]() )若
)若![]() ,求
,求![]() 的前
的前![]() 项和.
项和.
(![]() )设数列
)设数列![]() 为等差数列,证明:
为等差数列,证明: ![]() 或者
或者![]() (
(![]() 为常数),
为常数),![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() )设数列
)设数列![]() 为等差数列,公差为
为等差数列,公差为![]() ,且
,且![]() .
.
记![]() ,
,
求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
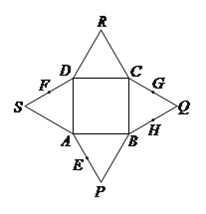
【题目】如图,已知四边形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等边三角形,
都是等边三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 、
、![]() 的中点,分别以
的中点,分别以![]() 、
、![]() 、
、![]() 、
、![]() 为折痕将四个等边三角形折起,使得
为折痕将四个等边三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点重合于一点
四点重合于一点![]() ,得到一个四棱锥.对于下面四个结论:
,得到一个四棱锥.对于下面四个结论:
①![]() 与
与![]() 为异面直线; ②直线
为异面直线; ②直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com