
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的最大面积是
的最大面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆E经过椭圆的左、右焦点,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,
三点共线,![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,且
,且![]() .
.
(i) 求直线![]() 的斜率;
的斜率;
(ii)当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;(ii)
;(ii)![]() .
.
【解析】
(1)根据离心率建立等式,结合![]() 的最大面积是
的最大面积是![]() 可求椭圆的方程;
可求椭圆的方程;
(2)(i)利用圆的对称性可得圆心![]() 为
为![]() 轴上一点,结合
轴上一点,结合![]() ,
,![]() ,
,![]() 三点共线可以表示出
三点共线可以表示出![]() 点的坐标,代入椭圆方程可求
点的坐标,代入椭圆方程可求![]() 点,进而可得直线
点,进而可得直线![]() 的斜率;
的斜率;
(ii)设出直线![]() 的方程,求出弦长,利用点到直线的距离公式求出三角形的高,结合面积公式及二次函数知识可求直线
的方程,求出弦长,利用点到直线的距离公式求出三角形的高,结合面积公式及二次函数知识可求直线![]() 的方程.
的方程.
(1)∵离心率![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() 面积的最大值为:
面积的最大值为:![]() ,
,
∴![]() ,
,![]() ;
;
∴椭圆方程为![]() .
.
(2)(i)∵圆![]() 经过椭圆的两个焦点,
经过椭圆的两个焦点,
∴圆心![]() 为
为![]() 轴上一点,设点
轴上一点,设点![]() ,
,
∵圆![]() 与椭圆在第一象限交于点
与椭圆在第一象限交于点![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,![]() 三点共线,且
三点共线,且![]() 是圆
是圆![]() 的一条直径,
的一条直径,
∴![]() ,
,
将![]() 点代入椭圆方程得到
点代入椭圆方程得到![]() ,即
,即![]() ,
,
∴直线![]() 的斜率为
的斜率为 .
.
(ii)∵![]() ,∴直线
,∴直线![]() 的斜率也为
的斜率也为![]() ,设直线
,设直线![]() ,
,![]() ,
,
联立 ,得
,得![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
点![]() 到直线
到直线![]() :
:![]() 的距离
的距离![]() ,
,
∴![]()
![]() .
.
∴当![]() ,即
,即![]() 时
时![]() 的面积最大,此时直线
的面积最大,此时直线![]() 的方程为:
的方程为:![]() .
.


科目:高中数学 来源: 题型:
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)根据数据用最小二乘法求出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() (系数用分数表示,不能用小数);
(系数用分数表示,不能用小数);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:(1)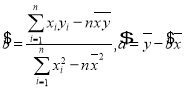 (2)
(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年春节期间全国流行在微信群里发、抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如表:

(I)求产生的手气红包的金额不小于9元的频率;
(Ⅱ)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)在这50个红包组成的样本中,将频率视为概率.
(i)若红包金额在区间[21,25]内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
(ii)随机抽取手气红包金额在[1,5)∪[﹣21,25]内的两名幸运者,设其手气金额分别为m,n,求事件“|m﹣n|>16”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 存在极值,求实数a的取值范围;
存在极值,求实数a的取值范围;
(2)设![]() ,设
,设![]() 是定义在
是定义在![]() 上的函数.
上的函数.
(ⅰ)证明:![]() 在
在![]() 上为单调递增函数(
上为单调递增函数(![]() 是
是![]() 的导函数);
的导函数);
(ⅱ)讨论![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某街区道路示意图,图中的实线为道路,每段道路旁的数字表示单向通过此段道路时会遇见的行人人数,在防控新冠肺炎疫情期间,某人需要从A点由图中的道路到B点,为避免人员聚集,此人选择了一条遇见的行人总人数最小的从A到B的行走线路,则此人从A到B遇见的行人总人数最小值是_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明代商人程大位在公元1592年编撰完成《算法统宗》一书.书中有如下问题:“今有女子善织,初日迟,次日加倍,第三日转速倍增,第四日又倍增,织成绢六丈七尺五寸.问各日织若干?”意思是:“有一位女子善于织布,第一天由于不熟悉有点慢,第二天起每天织的布都是前一天的2倍,已知她前四天共织布6丈7尺5寸,问这位女子每天织布多少?”根据文中的已知条件,可求得该女了第一天织布________尺,若织布一周(7天),共织________尺.(其中1丈为10尺,1尺为10寸)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点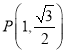 ,设它的左、右焦点分别为
,设它的左、右焦点分别为![]() 、
、![]() ,左顶点为
,左顶点为![]() ,上顶点为
,上顶点为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求椭圆![]() 的标准方程和离心率;
的标准方程和离心率;
(Ⅱ)过点![]() 作不与
作不与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() (异于点
(异于点![]() )两点,试判断
)两点,试判断![]() 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com