
| A�� | ��-$\frac{3}{2}$��-$\frac{18}{5}$�� | B�� | ��$\frac{4}{3}$��-$\frac{4}{3}$�� | C�� | ��-2��-4�� | D�� | ��$\frac{3}{2}$��-$\frac{6}{5}$�� |
���� ������ߵ���ͨ���̣���ֱ�߷����������������ֱ��l������C�صõ��߶��е�����꣮
��� �⣺����C�IJ�������Ϊ$\left\{\begin{array}{l}{x=5cos��}\\{y=4sin��}\end{array}\right.$����Ϊ����������ͨ����Ϊ$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1��
���㣨3��0����б��Ϊ$\frac{4}{5}$��ֱ��l�ķ���Ϊy=$\frac{4}{5}$��x-3����
����$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1�������ɵ�x2-3x-8=0��
����㣨3��0����б��Ϊ$\frac{4}{5}$��ֱ��l������C�صõ��߶��е�ĺ�����Ϊ$\frac{3}{2}$��
����y=$\frac{4}{5}$��x-3�����ɵ�������Ϊ-$\frac{6}{5}$��
��ѡ��D��
���� ���⿼�������������ͨ���̵�ת��������Τ�ﶨ�������ã������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
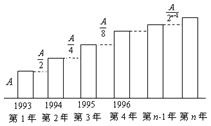 �ס����������繫˾��1993����г�ռ���ʾ�ΪA�������г�������Ԥ�⣬�ס��ҹ�˾��1993����������г�ռ���ʶ��������ӣ���˾��1993����������г�ռ���ʶ���ǰһ���$\frac{A}{2}$���ҹ�˾��1993����������г�ռ������ͼ��ʾ��
�ס����������繫˾��1993����г�ռ���ʾ�ΪA�������г�������Ԥ�⣬�ס��ҹ�˾��1993����������г�ռ���ʶ��������ӣ���˾��1993����������г�ռ���ʶ���ǰһ���$\frac{A}{2}$���ҹ�˾��1993����������г�ռ������ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | x1 | x2 | x3 | x4 | 5 |
| y | 2.5 | 4.6 | 5.4 | n | 7.5 |
| A�� | 9 | B�� | 8 | C�� | 7 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com