
【题目】已知直线![]() 的方程为
的方程为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点,点
距离最小的点,点![]() 是抛物线上异于点
是抛物线上异于点![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线与抛物线
轴平行的直线与抛物线![]() 交于点
交于点![]() .
.

(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)证明直线![]() 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)到直线![]() 距离最小的点,可根据点到直线距离公式,取最小值时的点;也可根据几何意义得为与直线
距离最小的点,可根据点到直线距离公式,取最小值时的点;也可根据几何意义得为与直线![]() 平行且与抛物线相切的切点:如根据点
平行且与抛物线相切的切点:如根据点![]() 到直线
到直线![]() 的距离
的距离
 得当且仅当
得当且仅当![]() 时取最小值,(Ⅱ)解析几何中定点问题的解决方法,为以算代证,即先求出直线AB方程,根据恒等关系求定点.先设点
时取最小值,(Ⅱ)解析几何中定点问题的解决方法,为以算代证,即先求出直线AB方程,根据恒等关系求定点.先设点![]()
![]() ,求出直线AP方程
,求出直线AP方程![]() ,与直线
,与直线![]() 方程联立,解出点
方程联立,解出点![]() 纵坐标为
纵坐标为![]() .即得
.即得![]() 点的坐标为
点的坐标为 ,再根据两点式求出直线AB方程
,再根据两点式求出直线AB方程![]() ,最后根据方程对应
,最后根据方程对应![]() 恒成立得定点
恒成立得定点![]()
试题解析:(Ⅰ)设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
所以,点![]() 到直线
到直线![]() 的距离
的距离
 .
.
当且仅当![]() 时等号成立,此时
时等号成立,此时![]() 点坐标为
点坐标为![]() .………………………………4分
.………………………………4分
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,显然
,显然![]() .
.
当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为 ,
,
化简得![]() ;
;
综上,直线![]() 的方程为
的方程为![]() .
.
与直线![]() 的方程
的方程![]() 联立,可得点
联立,可得点![]() 的纵坐标为
的纵坐标为![]() .
.
因为,![]() 轴,所以
轴,所以![]() 点的纵坐标为
点的纵坐标为![]() .
.
因此,![]() 点的坐标为
点的坐标为 .
.
当![]() ,即
,即![]() 时,直线
时,直线![]() 的斜率
的斜率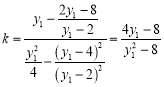 .
.
所以直线![]() 的方程为
的方程为![]() ,
,
整理得![]() .
.
当![]() ,
,![]() 时,上式对任意
时,上式对任意![]() 恒成立,
恒成立,
此时,直线![]() 恒过定点
恒过定点![]() ,
,
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,仍过定点
,仍过定点![]() ,
,
故符合题意的直线![]() 恒过定点
恒过定点![]() .……………………………………13分
.……………………………………13分


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,
,![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设函数![]() 有两个极值点
有两个极值点![]() ,
,![]() 且
且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程.
已知曲线![]() 的参数方程为
的参数方程为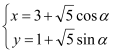 (
(![]() 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线的极坐标方程为![]() ,求直线被曲线
,求直线被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上有最大值1和最小值0,设
上有最大值1和最小值0,设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() (
(![]() 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
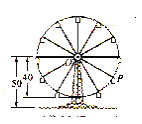
【题目】如图所示,摩天轮的半径为![]() 米,点
米,点![]() 距地面高度为
距地面高度为![]() 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每![]() 分钟转一圈,以点
分钟转一圈,以点![]() 为原点,过点
为原点,过点![]() 且平行与地平线的直线为
且平行与地平线的直线为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,设点
,设点![]() 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻![]() (分钟)时点
(分钟)时点![]() 距地面的高度
距地面的高度![]() (米),则
(米),则![]() 与
与![]() 的函数关系式
的函数关系式
![]()
![]() __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点![]() 到地面的距离不小于
到地面的距离不小于![]() 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10道题,其中6道甲类题,4道乙类题,小明同学从中任取3道题解答.
(Ⅰ)求小明同学至少取到1道乙类题的概率;
(Ⅱ)已知所取的3道题中有2道甲类题,1道乙类题.若小明同学答对每道甲类题的概率都是![]() ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是![]() ,且各题答对与否相互独立.求小明同学至少答对2道题的概率.
,且各题答对与否相互独立.求小明同学至少答对2道题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从全班![]() 名男同学,
名男同学, ![]() 名女同学中随机抽取一个容量为
名女同学中随机抽取一个容量为![]() 的样本进行分析.
的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出计算式即可,不必计算出结果)
(2)随机抽取![]() 位,他们的数学分数从小到大排序是:
位,他们的数学分数从小到大排序是: ![]() ,物理分数从小到大排序是:
,物理分数从小到大排序是: ![]() .
.
①若规定![]() 分以上(包括
分以上(包括![]() 分)为优秀,求这
分)为优秀,求这![]() 位同学中恰有
位同学中恰有![]() 位同学的数学和物理分数均为优秀的概率;
位同学的数学和物理分数均为优秀的概率;
②若这![]() 位同学的数学、物理分数事实上对应如下表:
位同学的数学、物理分数事实上对应如下表:

根据上表数据,由变量![]() 与
与![]() 的相关系数可知物理成绩
的相关系数可知物理成绩![]() 与数学成绩
与数学成绩![]() 之间具有较强的线性相关关系,现求
之间具有较强的线性相关关系,现求![]() 与
与![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ).
).
参考公式:回归直线的方程是: ![]() ,其中对应的回归估计值
,其中对应的回归估计值 ,
,
参考数据: ![]() ,
, ![]() ,
, ![]() ,,
,, ![]() ,.
,.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com