

图10-20
(1)证明:AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明:面AED⊥面A1FD1;
(文)(4)设AA1=2,求三棱锥E-AA1F的体积V![]() .
.
(1)![]() ;
;
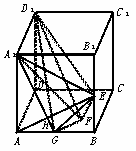
图10-53
(2)如图10-53,取AB中点G,连A1G、FG,因为F是CD中点,所以CF![]() AD,又A1D1
AD,又A1D1![]() AD,
AD,
所以GF![]() A1D1,故GFD1A1是平行四边形,A1G∥D1F.
A1D1,故GFD1A1是平行四边形,A1G∥D1F.
设A1G与AE交于点H,则∠AHA1是AE与D1F所成的角,因E是BB1中点,所以Rt△A1AG≌Rt△ABE,
∠GA1A=∠GAH,从而∠AHA1=90°,即直线AE与D1F所成角为直角.
(3)由(1)知AD⊥D1F,由(2)知AE⊥D1F,又AD∩AE=A,所以D1F⊥面AED,又D1F![]() 面A1FD1,
面A1FD1,
所以面AED⊥面A1FD1.
(文)(4)∵体积VE-AA1F=VF-AA1E
又FG⊥面ABB1A1,三棱锥F-AA1E的高FG=AA1=2,
面积S△AA1E=![]() S平行四边形ABB1A1=
S平行四边形ABB1A1=![]() ×22=2
×22=2
∴VE-AA1F=![]() ×S△AA1E×FG=
×S△AA1E×FG=![]() ×2×2=
×2×2=![]()
评述:本题主要考查棱柱的概念、两异面直线的垂直、异面直线所成的角、两平面垂直等能力方面主要考查空间想象能力、逻辑思维能力和运算能力此题中的四个小问题层层深入,由(1)的证明线线垂直到(2)中用到了线面垂直,而证得(3)中的面面垂直,最后在(4)中求体积脉络清楚,考查立几知识较全面注意在后一小问题中用到前面小题的结论这在立几大题中经常出现求体积过程中对三棱锥的顶点和底面作了灵活的转换,使计算简单,这也是求三棱锥体积的常用方法.


科目:高中数学 来源: 题型:
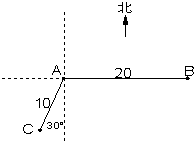 如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.
如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.
| ||
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
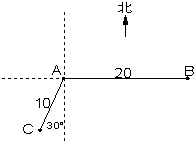 如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.
如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.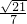 ).
).查看答案和解析>>
科目:高中数学 来源: 题型:

图10
查看答案和解析>>
科目:高中数学 来源: 题型:

图10-20
(1)证明:AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明:面AED⊥面A1FD1;
(理)(4)设AA1=2,求三棱锥F-A1ED1的体积V![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com