【答案】
分析:根据α为锐角和sin(

)的值,得到

的范围,利用同角三角函数间的基本关系即可求出cos(

)的值,然后根据二倍角的正弦函数公式求出sin(2α-

)的值,再根据诱导公式及正弦函数为奇函数即可得到cos2α的值.
解答:解:∵

,
∴

,
∴

,
所以cos(

)=

=

,
∴sin(2α-

)=2sin(α-

)cos(α-

)=2×
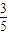
×

=

,
则cos2α=sin(

-2α)=-sin(2α-

)=-

.
故选A
点评:此题考查学生灵活运用同角三角函数间的基本关系化简求值,灵活运用二倍角的正弦函数公式及诱导公式化简求值,掌握正弦函数的奇偶性和单调性,是一道基础题.求出

的范围是解本题的关键.

 ,则cos2α=( )
,则cos2α=( )


