
分析 先证$\frac{lnn}{{n}^{2}}$<$\frac{1}{n\sqrt{n}}$,?$\frac{ln\sqrt{n}}{\sqrt{n}}$<$\frac{1}{2}$,设f(x)=$\frac{lnx}{x}$(x≥1),求出导数,运用单调性可得最大值,可证;再证$\frac{1}{n\sqrt{n}}$<2($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$),n≥2.运用裂项和放缩法可得,再由累加法即可得证.
解答 证明:先证$\frac{lnn}{{n}^{2}}$<$\frac{1}{n\sqrt{n}}$?$\frac{lnn}{n}$<$\frac{1}{\sqrt{n}}$?lnn<$\sqrt{n}$
?2ln$\sqrt{n}$<$\sqrt{n}$?$\frac{ln\sqrt{n}}{\sqrt{n}}$<$\frac{1}{2}$,
设f(x)=$\frac{lnx}{x}$(x≥1),f′(x)=$\frac{1-lnx}{{x}^{2}}$,
当1<x<e时,f′(x)>0,f(x)递增;
当x>e时,f′(x)<0,f(x)递减.
即有x=e处取得最大值,且为$\frac{1}{e}$,
则$\frac{ln\sqrt{n}}{\sqrt{n}}$≤$\frac{1}{e}$<$\frac{1}{2}$,
再证$\frac{1}{n\sqrt{n}}$<2($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$),n≥2.
由$\frac{1}{n\sqrt{n}}$<$\frac{1}{n\sqrt{n-1}}$=$\frac{1}{\sqrt{n}•\sqrt{n}•\sqrt{n-1}}$=$\frac{1}{\sqrt{n}}$•$\frac{1}{\sqrt{n}-\sqrt{n-1}}$($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$)
=$\frac{1}{\sqrt{n}}$•($\sqrt{n}$+$\sqrt{n-1}$)($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$)<$\frac{2\sqrt{n}}{\sqrt{n}}$($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$)=2($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$),
则$\frac{1}{n\sqrt{n}}$<2($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$),n≥2.
即有$\frac{lnn}{{n}^{2}}$<2($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$),n≥2.
即有$\frac{ln2}{{2}^{2}}$<2(1-$\frac{1}{\sqrt{2}}$),$\frac{ln3}{{3}^{2}}$<2($\frac{1}{\sqrt{2}}$-$\frac{1}{\sqrt{3}}$),
…,$\frac{lnn}{{n}^{2}}$<2($\frac{1}{\sqrt{n-1}}$-$\frac{1}{\sqrt{n}}$),n≥2.
累加可得$\frac{ln2}{{2}^{2}}$+$\frac{ln3}{{3}^{2}}$+$\frac{ln4}{{4}^{2}}$+…+$\frac{lnn}{{n}^{2}}$<2(1-$\frac{1}{\sqrt{n}}$).
点评 本题考查不等式的证明,注意运用不等式的传递性和累加法,以及裂项和放缩法证明,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
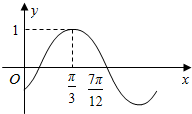 已知函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则 ( )
已知函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则 ( )| A. | ω=1,φ=$\frac{π}{6}$ | B. | ω=1,φ=-$\frac{π}{6}$ | C. | ω=2,φ=$\frac{π}{6}$ | D. | ω=2,φ=-$\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com