
【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.![]()
C.(1,3]
D.(1,5]
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给出下列结论: ①已知函数f(x)是定义在R上的奇函数,若f(﹣1)=2,f(﹣3)=﹣1,则f(3)<f(﹣1);
②函数y=log ![]() (x2﹣2x)的单调递增减区间是(﹣∞,0);
(x2﹣2x)的单调递增减区间是(﹣∞,0);
③已知函数f(x)是奇函数,当x≥0时,f(x)=x2 , 则当x<0时,f(x)=﹣x2;
④若函数y=f(x)的图象与函数y=ex的图象关于直线y=x对称,则对任意实数x,y都有f(xy)=f(x)+f(y).
则正确结论的序号是(请将所有正确结论的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)随机误差e是衡量预报精确度的一个量,它满足E(e)=0
(2)残差平方和越小的模型,拟合的效果越好;
(3)用相关指数R2来刻画回归的效果时,R2的值越小,说明模型拟合的效果越好;
(4)直线y=bx+a和各点(x1 , y1),(x2 , y2),…,(xn , yn)的偏差 ![]() 是该坐标平面上所有直线与这些点的偏差中最小的直线.
是该坐标平面上所有直线与这些点的偏差中最小的直线.
其中真命题的个数( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是二次函数,方程f(x)=0有两相等实根,且f′(x)=2x+2
(1)求f(x)的解析式.
(2)求函数y=f(x)与y=﹣x2﹣4x+1所围成的图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
: 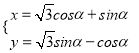 (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)曲线![]() 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线![]() 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com