
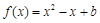 ,且
,且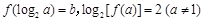 .
.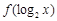 的最小值及对应的x值;
的最小值及对应的x值;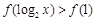 的解集记为A,不等式
的解集记为A,不等式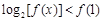 的解集记为B,求
的解集记为B,求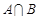 .
.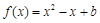
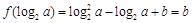 ,∴
,∴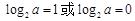

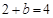 ∴
∴ b
b =" 2······························································" 4分
=" 2······························································" 4分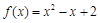 ,
,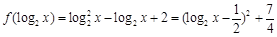
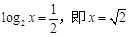 时,
时,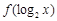 的最小值为
的最小值为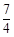 ······························· 6分
······························· 6分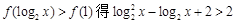
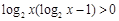
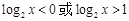
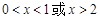 ,即
,即 ······································· 9分
······································· 9分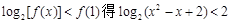
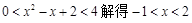
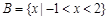 ······································································· 11分
······································································· 11分 ···································································· 12分
···································································· 12分

科目:高中数学 来源:不详 题型:单选题
 ,那么( )
,那么( )| A.当x∈(1,+∞)时,函数单调递增 |
| B.当x∈(1,+∞)时,函数单调递减 |
| C.当x∈(-∞,-1)时,函数单调递增 |
| D.当x∈(-∞,3)时,函数单调递减 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B.(-∞,-3) | C.(-∞,-3] | D.[3,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,g¢(x),且
,g¢(x),且 ="0,"
="0,"  =?2,f(1)="g(1),"
=?2,f(1)="g(1),"  =g¢(1).
=g¢(1).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
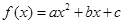 的图象开口向下,对称轴为x=1,图象与x轴的两个交点中,一个交点的横坐标
的图象开口向下,对称轴为x=1,图象与x轴的两个交点中,一个交点的横坐标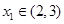 ,则以下结论中:
,则以下结论中:查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com