
【题目】如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点. 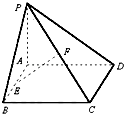
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若∠PDA=45°,求EF与平面ABCD所成的角的大小.
【答案】
(1)解:取PD中点Q,连AQ、QF,则AE∥QF
∴四边形AEFQ为平行四边形
∴EF∥AQ
又∵AQ在平面PAD内,EF不在平面PAD内
∴EF∥面PAD
(2)解:证明∵CD⊥AD,CD⊥PA,PA∩AD=A
PA在平面PAD内,AD在平面PAD内
∴CD⊥面PAD
又∵AQ在平面PAD同
∴CD⊥AQ
∵EF∥AQ
∴CD⊥EF
(3)解:解∵∠PDA=45°
∴△PAD为等腰直角三角形
∴AQ⊥PD
∴∠QAD=45°
即AQ与平面ABCD所成角为45°
又∵AQ∥EF
∴EF与平面ABCD所成角45°.
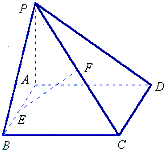
【解析】(1)取PD中点Q,连AQ、QF,易证EF∥AQ,根据直线与平面平行的判定定理可证得EF∥面PAD;(2)欲证CD⊥EF,可先证直线与平面垂直,CD⊥AD,CD⊥PA,PA∩AD=A,根据直线与平面垂直的判定定理可知CD⊥面PAD,从而得到CD⊥EF;(3)先证∠QAD为AQ与平面ABCD所成角,在三角形QAD中求出此角,再根据AQ∥EF,得到EF与平面ABCD所成的角的大小.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则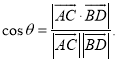 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知a,b,c成等比数列,且 ![]() .
.
(Ⅰ)求角B的大小;
(Ⅱ)若b=3,求△ABC的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(Ⅰ)求f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的函数,对任意实数m,n,都有f(m)f(n)=f(m+n),且当x<0时,0<f(x)<1.
(1)证明:①f(0)=1;②当x>0时,f(x)>1;③f(x)是R上的增函数;
(2)设a∈R,试解关于x的不等式f(x2﹣3ax+1)f(﹣3x+6a+1)≤1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸线![]() 一侧
一侧![]() 处有一个美丽的小岛,某旅游公司为方便游客,在
处有一个美丽的小岛,某旅游公司为方便游客,在![]() 上设立了
上设立了![]() 两个报名点,满足
两个报名点,满足![]() 中任意两点间的距离为
中任意两点间的距离为![]() .公司拟按以下思路运作:先将
.公司拟按以下思路运作:先将![]() 两处游客分别乘车集中到
两处游客分别乘车集中到![]() 之间的中转点
之间的中转点![]() 处(点
处(点![]() 异于
异于![]() 两点),然后乘同一艘轮游轮前往
两点),然后乘同一艘轮游轮前往![]() 岛.据统计,每批游客
岛.据统计,每批游客![]() 处需发车2辆,
处需发车2辆, ![]() 处需发车4辆,每辆汽车每千米耗费
处需发车4辆,每辆汽车每千米耗费![]() 元,游轮每千米耗费
元,游轮每千米耗费![]() 元.(其中
元.(其中![]() 是正常数)设∠
是正常数)设∠![]() ,每批游客从各自报名点到
,每批游客从各自报名点到![]() 岛所需运输成本为
岛所需运输成本为![]() 元.
元.
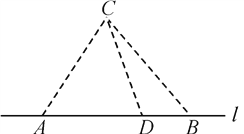
(1) 写出![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
(2) 问:中转点![]() 距离
距离![]() 处多远时,
处多远时, ![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)分别求第3,4,5组的频率.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场宣传活动,应从第3,4,5组各抽取多少名志愿者?
(3)在(2)的条件下,我市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com