
【题目】已知过点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于M,N两点.
交于M,N两点.
(Ⅰ)设线段MN的中点为P,求点P的轨迹方程;
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为
为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 所在的直线方程.
所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
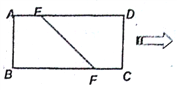
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,将四边形
,将四边形![]() 沿
沿![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上.
上.
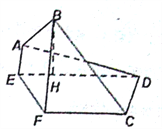
(I)求证: ![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离;
的距离;
(III)求直线![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广东省深圳市高三下学期第一次调研考试(一模)数学理】已知函数![]() 为自然对数的底数.
为自然对数的底数.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的值;
的值;
(3)关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足:|a2-a3|=10,a1a2a3=125.
(1) 求{an}的通项公式;
(2) 求证:![]() +
+![]() +…+
+…+![]() <1对任意正整数m都成立.
<1对任意正整数m都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() .计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
.计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com