（13分）定义在R上的增函数y=f(x)对任意x,y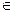
R都有f(x+y)=f(x)+f(y),则
（1）求f(0) (2) 证明：f(x)为奇函数
(3)若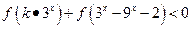
对任意
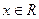恒成立，求实数k的取值范围
名校课堂系列答案科目：高中数学 来源： 题型：解答题
(本题满分12分)二次函数f(x)的最小值为1，且f(0)＝f(2)＝3.
(1)求f(x)的解析式；(2)若f(x)在区间[2a，a＋1]上不单调，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(12分)(2010·无锡模拟)已知f(x)在定义域(0，＋∞)上为增函数，且满足f(xy)＝f(x)＋f(y)，f(3)＝1，试解不等式f(x)＋f(x－8)≤2.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某商家经销一种销售成本
为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500kg；销售单价每涨1元，月销售量就减少10kg，针对这种销售情况，
（1）设销售单价为每千克x元，月销售利润
为y元，求y与x的函数关系式；
商店想在月销售成本不超过10000元的情况下，使得月销售利润不少于8000元，销售单价应定为多少元时，利润最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，得f(x-x)=f(x)+f(-x),又f（0）=0,则有0=f(x)+f(-x),即可证得………7分
即有
得
，又有
，所以只要使
………13分
在定义域
上为增函数，且满足
, 
.
的值; 
.
）已知
是定义在
上的奇函数，且
时，
． 
，
，求
的取值
范围
；
，求
的值。
的定义域为
，并满足以下条件：①对任意的
；
，都有
；③
.
的值；
是
上的单调递增函数；
的不等式：
的图
象.
时函数的值域