
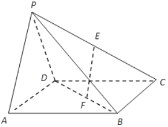
【题目】在四棱锥中![]() ,底面
,底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,且
,且![]() ,分别为
,分别为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,若存在,请求出点
,若存在,请求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]() 为
为![]() 的中点.
的中点.
【解析】
试题分析:(1)根据题意可连接![]() ,与
,与![]() 相交于点
相交于点![]() ,易证
,易证![]() ,根据线面平行的判定定理即可证得
,根据线面平行的判定定理即可证得![]() 平面
平面![]() ;(2)取
;(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,可证得
,可证得![]() 平面
平面![]() ,以
,以![]() 为原点,分别以射线
为原点,分别以射线![]() 和
和![]() 为
为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,不妨设
,不妨设![]() ,
,![]()
![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的法向量,根据二面角的求法得到
的法向量,根据二面角的求法得到![]() 的方程,求出其值,若满足
的方程,求出其值,若满足![]() ,则存在,否则不存在.
,则存在,否则不存在.
试题解析:(1)证明:连接![]() ,由正方形性质可知,
,由正方形性质可知,![]() 与
与![]() 相交于点
相交于点![]() ,
,
所以,在![]() 中,
中,![]() .........................1分
.........................1分
又![]() 平面
平面![]() 平面
平面![]() .....................3分
.....................3分
所以![]() 平面
平面![]() ...................4分
...................4分
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,所以
,所以![]() 平面
平面![]() ,
,
以![]() 为原点,分别以射线
为原点,分别以射线![]() 和
和![]() 为
为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,不妨设
,不妨设![]() ................ 6分
................ 6分
则有![]() ,假设在
,假设在![]() 上存在点
上存在点![]() ,
,
则![]() .............. 7分
.............. 7分
因为侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,且底面是正方形,
,且底面是正方形,
所以![]() 平面
平面![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,
,
所以![]()
![]() ,即平面
,即平面![]() 的一个法向量为
的一个法向量为![]() .............. 8分
.............. 8分
设平面![]() 的法向理为
的法向理为![]() ,由
,由 即
即![]() ,亦即
,亦即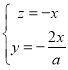 ,可取
,可取![]() ....................9分
....................9分
所以 ...................... 10分
...................... 10分
解得![]() (舍去)................................11分
(舍去)................................11分
所以线段![]() 上存在点
上存在点![]() ,且
,且![]() 为
为![]() 的中点,使得二面角
的中点,使得二面角![]() 的余弦值为
的余弦值为![]() .......12分
.......12分


科目:高中数学 来源: 题型:
【题目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若a>0,且A∩B=![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是![]() ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是![]() .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记![]() 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整:并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(2)针对于问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中男生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ;
;
(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(I)求f(0)的值和实数m的值;
(II)当m=1时,判断函数f(x)在(﹣1,1)上的单调性,并给出证明;
(III)若![]() 且f(b﹣2)+f(2b﹣2)>0,求实数b的取值范围.
且f(b﹣2)+f(2b﹣2)>0,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com