设

,函数

,

.
(I)试讨论函数

的单调性
(II)设

,求证:

有三个不同的实根.
当
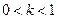
时,函数

在
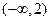
上递减,在
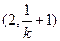
上递增,在
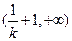
上递减;
当
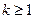
时,函数

在
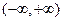
上是减函数;
当
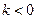
时,函数

在
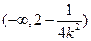
上递增,在
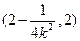
上递减,在
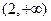
上递增.
解:(Ⅰ)∵
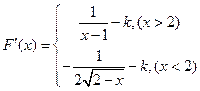
. ……………2分
∴当
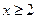
时,方程
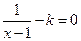
的解为:
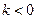
或
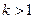
时无解,
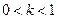
时为
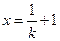
,
当
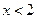
时,方程
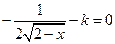
的解为:
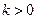
时无解,
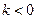
时为
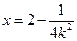
.
∴当
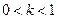
时,函数

在
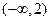
上递减,在
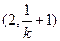
上递增,在
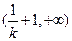
上递减;
当
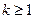
时,函数

在
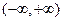
上是减函数;
当
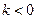
时,函数

在
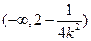
上递增,在
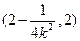
上递减,在
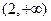
上递增. ……………7分
(Ⅱ)∵
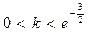
,由(Ⅰ)可知,

的取值随着
x的变化如下:

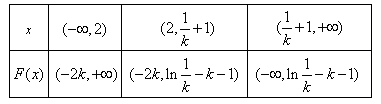
∴当
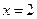
时,

极小值为
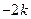
,
当
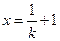
,

极大值为
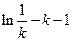
. ……………10分
∵
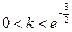
,∴
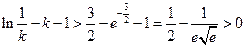
,
∴

极小
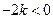
,

极大值为
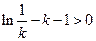
,
因此,
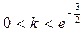
时,方程

一定有三个不同的实根.…………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
若函数
f(
x)=
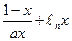
在[1,+∞
上为增函数.
(Ⅰ)求正实数
a的取值范围.
(Ⅱ)若
a=1,求征:
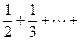
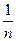
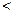
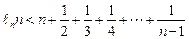
(
n∈N*且
n ≥ 2 )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数

.
(1)若
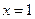
是函数

的一个极值点,试求出

关于

的关系式(用

表示

),并确定

的单调区间;
(2)在(1)的条件下,设

,函数

.若存在

使得

成立,求

的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分10分)
已知函数
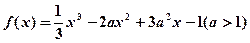
。
(1)当
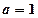
时,求函数
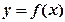
的单调增区间;
(2)若对任意
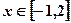
, 恒有
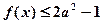
,求
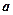
的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知函数
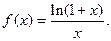
(1)确定
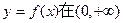
上的单调性;
(2)设
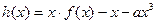
在(0,2)上有极值,求
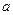
的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
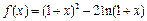
.
(Ⅰ)求
f (
x)的单调区间;
(Ⅱ)若当
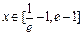
时,不等式
f (
x)<
m恒成立,求实数
m的取值范围;
(Ⅲ)若关于
x的方程
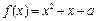
在区间[0, 2]上恰好有两个相异的实根,求实数
a的取值范围.
查看答案和解析>>

 ,函数
,函数 ,
, .
. 的单调性
的单调性 ,求证:
,求证: 有三个不同的实根.
有三个不同的实根. 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 .
.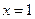 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出 关于
关于 的关系式(用
的关系式(用 表示
表示 ),并确定
),并确定 的单调区间;
的单调区间; ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.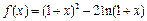 .
.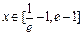 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;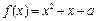 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.