设数列{an}的前n项和为Sn,已知a1=a(a≠3),Sn+1=2Sn+3n,n∈N*.
(1)设bn=Sn-3n,n∈N*,证明数列{bn}为等比数列;
(2)求数列{an}的通项公式;
(3)若an+1≥an,n∈N*,求a的取值范围.
解:(1)当a≠3时,

=2
所以{b
n}为等比数列. (4分)
(2)b
1=S
1-3=a-3,(1分)b
n=(a-3)×2
n-1. (2分)
所以S
n-3
n=(a-3)×2
n-1(3分)a
n=S
n-S
n-1,n≥2,n∈N
*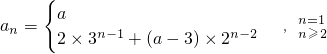
; (6分)
(3)a
n+1≥a
n,
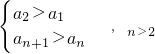
,(2分)
a≥-9(5分)
所以a≥-9,且a≠3. (6分)
分析:(1)由已知中S
n+1=2S
n+3
n,b
n=S
n-3
n,n∈N
*,我们可以得到

为定值2,根据等比数列的定义,即可得到数列{b
n}为等比数列;
(2)由(1)中结论,我们易求出数列{b
n}的通项公式,进而得到S
n的表达式,进而根据a
n=S
n-S
n-1,n≥2,可以求出数列{a
n}的通项公式;
(3)根据数列a
n+1≥a
n,n∈N
*,我们可(2)中数列{a
n}的通项公式,构造出一个关于a的不等式组,解不等式组,即可得到a的取值范围.
点评:本题考查的知识点是等比关系的确定,数列的函数特征,数列递推式,其中(1)的关键是根据等比数列的定义,证得

为定值,但要注意由限制首项不为0,(2)的关键是根据a
n=S
n-S
n-1,n≥2求通项,要注意对n=1时的判断;(3)的关键是根据(2)的结论,构造关于a的不等式组,同样要注意a
1<a
2

 =2
=2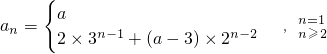 ; (6分)
; (6分)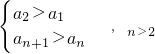 ,(2分)
,(2分) 为定值2,根据等比数列的定义,即可得到数列{bn}为等比数列;
为定值2,根据等比数列的定义,即可得到数列{bn}为等比数列; 为定值,但要注意由限制首项不为0,(2)的关键是根据an=Sn-Sn-1,n≥2求通项,要注意对n=1时的判断;(3)的关键是根据(2)的结论,构造关于a的不等式组,同样要注意a1<a2
为定值,但要注意由限制首项不为0,(2)的关键是根据an=Sn-Sn-1,n≥2求通项,要注意对n=1时的判断;(3)的关键是根据(2)的结论,构造关于a的不等式组,同样要注意a1<a2 
