
【题目】已知函数![]() .
.
(Ⅰ)过原点作曲线![]() 的切线,求切线方程;
的切线,求切线方程;
(Ⅱ)当![]() 时,讨论曲线
时,讨论曲线![]() 与曲线
与曲线![]() 公共点的个数.
公共点的个数.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当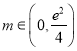 时,有0个公共点;当
时,有0个公共点;当![]() 时,有1个公共点;当
时,有1个公共点;当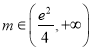 时,有2个公共点.
时,有2个公共点.
【解析】【试题分析】(1)依据题设借助导数的几何意义分析求解;(2)先将零点的个数化为方程根的个数,再将方程问题转化为函数的图像问题,最后通过构造函数,运用导数的知识分析求解:
(Ⅰ)由题意,设切点为![]() ,由题意可得
,由题意可得
![]() ,即
,即![]() ,解得
,解得![]() ,即切点
,即切点![]() .
.
所以![]() ,所以切线方程为
,所以切线方程为![]() .
.
(Ⅱ)当![]() ,
, ![]() 时,曲线
时,曲线![]() 与曲线
与曲线![]() 的公共点个数
的公共点个数
即方程![]() 根的个数.
根的个数.
由![]() 得
得![]() .
.
令![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]() .
.
随![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
| 2 |
|
| — | 0 | + |
| ↘ | 极小值 | ↗ |
其中![]() .所以
.所以![]() 为
为![]() 在
在![]() 的最小值.
的最小值.
所以对曲线![]() 与曲线
与曲线![]() 公共点的个数,讨论如下:
公共点的个数,讨论如下:
当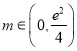 时,有0个公共点;当
时,有0个公共点;当![]() 时,有1个公共点;当
时,有1个公共点;当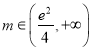 时,有2个公共点.
时,有2个公共点.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】甲、乙二人做射击游戏,甲、乙射击击中与否是相互独立事件.规则如下:若射击一次击中,则原射击人继续射击;若射击一次不中,就由对方接替射击.已知甲、乙二人射击一次击中的概率均为![]() ,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率____________;②求第4次由甲射击的概率________.
,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率____________;②求第4次由甲射击的概率________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
A小区 | 低碳族 | 非低碳族 |
比例 |
|
|
B小区 | 低碳族 | 非低碳族 |
比例 |
|
|
C小区 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)从A,B,C三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).以原点
).以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com