
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于
的图象交于![]() ,
, ![]() 两点,其中
两点,其中![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)首先求得切线斜率![]() ,且
,且![]() ,据此由点斜式写出切线方程
,据此由点斜式写出切线方程![]() .
.
(2)由令![]() ,得
,得![]() ,
, ![]() .分类讨论:
.分类讨论: ![]() ,
, ![]() ,
, ![]() ,三种情况即可得到函数的单调区间;
,三种情况即可得到函数的单调区间;
(3)经分析可知,证明原问题只需证明![]() ,构造函数
,构造函数![]() ,可证得
,可证得![]() ,即
,即![]() 得证.
得证.
试题解析:
(Ⅰ)当![]() 时,
时, ![]() (
(![]() ),
),
则![]() (
(![]() ),
),![]() .
.
又![]() ,所以切线方程为,即
,所以切线方程为,即![]() .
.
(Ⅱ)![]() ,令
,令![]() ,得
,得![]() ,
, ![]() .
.
①当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,
,
所以当![]() 时,
时, ![]() 单调增区间为
单调增区间为![]() 和
和![]() ;单调减区间为
;单调减区间为![]() .
.
②当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,
,
所以当![]() ,
, ![]() 单调增区间为
单调增区间为![]() 和
和![]() ;单调减区间为
;单调减区间为![]() .
.
③当![]() ,即
,即![]() 时,
时, ![]() ,
,
易知![]() 单调增区间为
单调增区间为![]() .
.
(Ⅲ)根据题意, ![]() .(以下用分析法证明)
.(以下用分析法证明)
要证![]() ,只要证
,只要证![]() ,
,
只要证![]() ,
,
令![]() ,则只需证:
,则只需证: ![]() ,令
,令![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
∴![]() ,即
,即![]() ,同理可证:
,同理可证: ![]() ,
,
综上, ![]() ,即
,即![]() 得证.
得证.


科目:高中数学 来源: 题型:
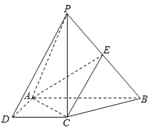
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:

其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间![]() (单位:小时)与年龄
(单位:小时)与年龄![]() (单位:岁),并制作了对照表(如下表所示)
(单位:岁),并制作了对照表(如下表所示)
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据,试求线性回归方程![]() ,并预测年龄为55岁观众周均学习成语知识时间.
,并预测年龄为55岁观众周均学习成语知识时间.
参考公式: 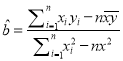 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:


将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的![]() 列联表,若按
列联表,若按![]() 的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 分布列,期望
分布列,期望![]() 和方差
和方差![]() .
.
附: 

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com