
 lnx,再求出此函数的导数及单调性,判断出函数值的符号,再由变化趋势求出a的范围.
lnx,再求出此函数的导数及单调性,判断出函数值的符号,再由变化趋势求出a的范围. =
= ,
, ,则0<
,则0< <a,
<a, )恒小于零,在(
)恒小于零,在( ,a)恒大于零,
,a)恒大于零, )递减,在(
)递减,在( ,a)递增
,a)递增 )=
)= ln
ln +(a-
+(a- )ln(a-
)ln(a- )=aln(
)=aln( )≤0,
)≤0, lnx,x>0,
lnx,x>0,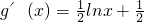 =0,得x=
=0,得x= ,
, )递减,在(
)递减,在( ,+∞)递增,
,+∞)递增, lnx<0,最小值g(
lnx<0,最小值g( )<0,
)<0, ln1=0,此时a=2,
ln1=0,此时a=2,

 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
| 1 | e |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春十一高高二(下)期初数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com