
【题目】如图所示,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,且
,且 ![]() ,
,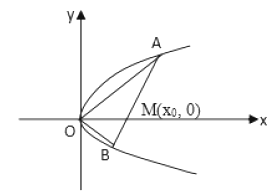
(1)求证:点 ![]() 的坐标为
的坐标为 ![]() ;
;
(2)求证: ![]() ;
;
(3)求 ![]() 面积的最小值.
面积的最小值.
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】一次数学考试后,某老师从甲,乙两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学成绩的中位数为73,则 ![]() 的值为( )
的值为( )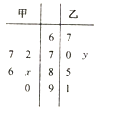
A.2
B.-2
C.3
D.-3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
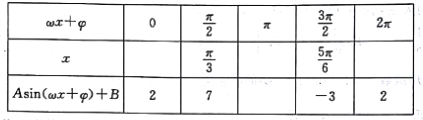
(I)请将上表数据补充完整,并直接写出函数![]() 的解析式
的解析式
(II)将![]() 的图像上所有点向左平行移动
的图像上所有点向左平行移动![]() 个单位长度,得到
个单位长度,得到![]() 的图像,求
的图像,求![]() 的图像离
的图像离![]() 轴最近的对称中心.
轴最近的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在30天内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段![]() ,
,![]() (不包含
(不包含![]() ,
,![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.
第 | 5 | 1 5 | 2 0 | 3 0 |
销售量 | 3 5 | 2 5 | 2 0 | 1 0 |
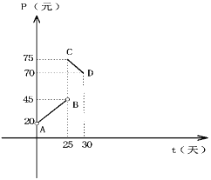
(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com