
分析 (1)△ABC中,由bcosC=(2a-c)cosB,利用正弦定理化简可得cosB=-$\frac{1}{2}$,即可求B;
(2)由正弦定理化简已知等式可得:a=3c,代入余弦定理即可得解.
解答 解:(1)△ABC中,∵2a•cosB+c•cosB+b•cosC=0,可得:-bcosC=(2a+c)cosB,由正弦定理得:
-2RsinBcosC=(4RsinA+2RsinC)cosB,即-sinBcosC-sinCcosB=2sinAcosB,
化简为-sin(B+C)=2sinAcosB,
∴-sinA=2sinAcosB,sinA≠0,
∴cosB=-$\frac{1}{2}$,
∴B=120°
(2)∵sinA=3sinC,
∴由正弦定理可得:a=3c,
∴由余弦定理b2=a2+c2-2accosB可得:13=9c2+c2-2×$3c×c×(-\frac{1}{2})$,整理可解得:c=1,故可得a=3.
点评 本题主要考查两角和差的正弦、余弦公式、正弦定理、和差化积公式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 抛物线x2=y(-2≤x≤2)绕轴旋转180°形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的上底面恰好与旋转体的开口面平齐,下底面的四个顶点落在曲面上,则此正方体的外接球的表面积为( )
抛物线x2=y(-2≤x≤2)绕轴旋转180°形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的上底面恰好与旋转体的开口面平齐,下底面的四个顶点落在曲面上,则此正方体的外接球的表面积为( )| A. | 4π | B. | 12π | C. | 16π | D. | 48π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是真命题 | D. | 命题p∨(?q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
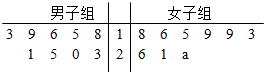
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com